Free math test papers for 4-th grade. Topics: “Numbers and Their Properties,” “Addition and Subtraction,” “Multiplication and Division,” “Geometry,” “Measurement and Units of Measurement,” “Multiplication Table,” “Logic Problems and Solutions”
Contents:
1. What should a child know in the subject before entering 4th grade?</br >
2. What should a child know in the subject upon completing 4th grade?</br >
3. Test No. 1 (1st quarter) on topics: “Digits of a Number,” “Multiplication and Division,” “Finding the Area and Perimeter of a Rectangle.”
4. Test No. 2 (1st quarter).
5. Test No. 3 (2nd quarter).
6. Test No. 4 (2nd quarter).
7. Test No. 5 (3rd quarter).
8. Tests No. 6 (3rd quarter).
9. Test No. 7 (4th quarter).
10. Test No. 8 (4th quarter).
11. Materials for preparing for tests. Review of the material covered last year.
12. Materials for preparing for tests. Solving problems on speed, time, and distance.
13. Materials for preparing for tests. Problems on finding the perimeter, area, and sides of geometric figures.
14. Answers to the tests.
Before entering 4th grade, a child should possess the following knowledge and skills:
1. Basic arithmetic operations: addition, subtraction, multiplication, and division of numbers up to 1000. For example, a child should be able to solve problems like: “If your friend earned 350 rubles, and you earned three times more, how much did you earn?”
2. Working with fractions: understanding the concepts of “half,” “quarter,” “third,” and using fractions with real examples. For example, you can ask: “Your mom cut the pie into 8 pieces. If you only ate 3 pieces, what fraction of the pie did you eat?”
3. Understanding decimal fractions: reading and writing numbers with a decimal point, converting a decimal fraction to a regular fraction and vice versa. For example, a child should understand that the number 0.5 is equal to 1/2, and the number 1/4 can be written as 0.25.
4. Working with geometric shapes: knowing the names and properties of simple shapes such as a circle, triangle, square, rectangle. For example, a child should be able to recognize these shapes in everyday life, such as in surrounding objects or buildings.
5. Measurement and comparison of quantities: understanding the concepts of greater, smaller, equal; ability to measure the length, mass, and volume of objects using different units of measurement. For example, a child should be able to say that a kilogram of apples is more than 500 grams of oranges.
6. Working with tables and graphs: ability to read and analyze data presented in tables or graphs. For example, a child should be able to compare the number of cinema tickets sold on different days of the week in a graph.
7. Solving word problems: ability to analyze problems, formulate equations, and solve them. For example, a problem may look like this: “There are 5 books on the table. If you add 2 books every day, how many books will be on the table after a certain number of days?”
8. Telling time and using the calendar: understanding time concepts, calculating time intervals, ability to read and determine the time on a clock dial. For example, a child should be able to say how much time has passed if the clock showed 2:30 and now it’s 5:00.
9. Understanding basic statistics concepts: ability to find the average and median of a numerical series. For example, a child should understand that the average score in the class is the sum of all scores divided by the number of students.
10. Basic understanding of probability: understanding the concept of possibility and impossibility of events, ability to estimate the probability of different outcomes. For example, a child should understand that the probability of getting heads when tossing a coin is 1/2, as there are two equally likely outcomes – heads or tails.
Program Requirements for Students upon Completion of the Fourth Grade Mathematics Course:
1. Ability to break down compound problems into parts.
2. Understanding and explaining problems involving motion (toward each other, in opposite directions, with delay).
3. Ability to create diagrams or explanatory diagrams for compound problems, use ready-made diagrams in problem-solving.
4. Finding the volume of figures composed of cubes or rectangular parallelepipeds.
5. When solving word problems, the ability to formulate and use given equations.
6. Ability to work (read information) with circular diagrams.
7. Finding the arithmetic mean of two and several numbers.
Test No. 1 on topics: “Digits of a Number,” “Multiplication and Division,” “Finding the Area and Perimeter of a Rectangle”
Variant I.
1. Represent these sentences in numerical form.
a) Nine hundred thirty.
b) Nine thousand one hundred.
c) Nineteen thousand three hundred four.
d) One hundred twenty-three thousand nine hundred ninety-nine.
2. Represent these expressions in numerical form. Write down the numbers that are located before and after these numbers in the numerical series.
a) Nine thousand nine hundred ninety-nine.
b) Five thousand.
c) Thirteen thousand five hundred three.
3. Perform the operations in columns.
| a)364 + 685 = | b) 102 + 586 = | c) 594 + 239 = |
| d) 495 – 299 = | e) 938 – 495 = | f) 596 – 343 = |
4. Solve the problems.
| a) 6 * 7 = | b) 8 * 9 = | c) 1 * 7 = | d) 0 * 5 = |
| e) 49 : 7 = | f) 9 : 1 = | g) 45 : 5 = | h) 18 : 3 = |
5. Solve the problem.
A tailor had 150 meters of fabric. He sewed 8 children’s and 6 adult suits. A children’s suit requires 5 meters of fabric, and an adult suit requires 13 meters. How many meters of fabric does the tailor have left after sewing the suits?
Variant II.
1. Represent these expressions in numerical form.
a) Eight hundred forty-five.
b) One hundred ninety-three thousand ninety.
c) Fifteen thousand four hundred five.
d) Three hundred forty-five thousand nine hundred ninety-nine.
2. Represent these expressions in numerical form. Write down the numbers that are located before and after these numbers in the numerical series.
a) Eight thousand nine hundred ninety-nine.
b) Seven thousand.
c) Ninety-three thousand five hundred ninety-nine.
3. Perform the operations in columns.
| a) 673 + 304 = | b) 145 + 723 = | c) 392 + 488 = |
| d) 495 – 107 = | e) 938 – 492 = | f) 896 – 402 = |
4. Solve the problems.
| a) 2 * 7 = | b) 8 * 8 = | c) 5 * 7 = | d) 1 * 5 = |
| e) 42 : 6 = | f) 9 : 3 = | g) 35 : 7 = | h) 18 : 9 = |
5. Solve the problem.
645 kg of flour were delivered to the warehouse. On the first day, 5 bags of 20 kg each were shipped, and on the second day, 12 bags of 25 kg each were shipped. How many kg of flour are left in the warehouse?
Variant III.
1. Represent these expressions in numerical form.
a) Nine hundred forty-one.
b) One hundred two thousand thirteen.
c) Sixteen thousand one.
d) Seventy-seven thousand three hundred.
2. Represent these expressions in numerical form. Write down the numbers that are located before and after these numbers in the numerical series.
a) Seventeen thousand nine hundred ninety-nine.
b) Twelve thousand.
c) Forty-five thousand eight.
3. Perform the operations in columns.
| a) 846 + 125 = | b) 391 + 359 = | c) 594 + 302 = |
| d) 837 – 107 = | e) 318 – 192 = | f) 685 – 452 = |
4. Solve the problems.
| a) 5 * 7 = | b) 6 * 3 = | c) 8 * 3 = | d) 4 * 5 = |
| e) 36 : 6 = | f) 21 : 3 = | g) 25 : 5 = | h) 12 : 6 = |
5. Solve the problem.
A craftsman makes a table in 4 days, and a nightstand in 3 days. In total, the craftsman made 12 tables and 18 nightstands. How much time did the craftsman spend making all this furniture?
Answers to Test No. 1 (1st quarter)
Test No. 2
Variant I.
1. Solve the problem.
Workers collected 8 bags of potatoes, each weighing 35 kg, from one field. From the second field, they collected 123 kg more. How many kilograms of potatoes did the workers collect from both fields?
2. Solve the problems.
| a) 852 – 204 * 3 + 187 = | b) 350 : (5 – 3) + 202 – 98 = |
| c) 720 : 8 + 627 – 567 = | d) 65 * (84 – 76) + 302 = |
3. Compare.
| a) 34 m 40 cm … 3441 cm | b) $5 ha … 5000 m^2$ |
| c) 58 km … 5800 m | d) 68 m 6 dm 4 mm … 69 m |
4. A rectangle is given with sides of 3 cm and 7 cm. Find its perimeter and area. Draw a square with the same perimeter and find its area.
5. Solve the problems.
| a) 356000 : 100 = | b) 928 * 1000 = |
| c) 65 * 1000 = | d) 7200 : 100 = |
6. Write down this data in descending order: 2 km; 600 dm; 349 mm; 1 m 59 cm; 15 dm 3 cm.
Variant II.
1. Solve the problem.
Vasya has 8 sets of postcards, with 7 cards in each set. Kolya has 18 fewer cards. How many cards do Vasya and Kolya have in total?
2. Solve the problems.
| a) 448 – 146 * 3 + 209 = | b) 320 : (6 – 4) + 429 – 298 = |
| c) 700 : 7 + 627 – 458 = | d) 72 * (92 – 88) – 145 = |
3. Compare.
| a) 2 m 43 cm … 240 cm | b) $5 ha 12 m^2$ … $512 m^2$ |
| c) 58 km 2 m… 5820 m | d) 68 m 4 mm … 6804 mm |
4. A rectangle is given with sides of 5 cm and 9 cm. Find its perimeter and area. Draw a square with the same perimeter and find its area.
5. Solve the problems.
| a) 38200 : 100 = | b) 567 * 100 = |
| c) 514 * 1000 = | d) 58000 : 1000 = |
6. Write down this data in ascending order: 12 mm; 2300 dm; 356 mm; 1 m 4 cm; 58 cm; 1 dm 9 cm.
Variant III.
1. Solve the problem.
Kolya has 6 sets of postcards, with 11 cards in each set. Misha has 14 fewer cards. How many cards do Kolya and Misha have in total?
2. Solve the problems.
| a) 578 – 168 * 3 + 256 = | b) 280 : (9 – 4) + 723 – 348 = |
| c) 640 : 8 + 452 – 338 = | d) 32 * (23 – 19) – 15 = |
3. Compare.
| a) 3 m 14 cm … 320 cm | b) $9 ha 1 m^2 … 902 m^2$ |
| c) 6 km 2 m… 6020 m | d) 67 m 5 mm … 6750 mm |
4. A rectangle is given with sides of 3 cm and 8 cm. Find its perimeter and area. Draw a square with the same perimeter and find its area.
5. Solve the problems.
| a) 44500 : 100 = | b) 523 * 100 = |
| c) 586 * 1000 = | d) 24000 : 1000 = |
6. Write down the magnitudes in ascending order: 16 mm; 7800 dm; 436 mm; 3 m 5 cm; 78 cm; 4 dm 7 cm.
Answers to Test No. 2 (1st quarter)
Test No. 3
Variant I.
1. Solve the problem.
A tractor driver plowed a field with an area of 420 hectares in 7 days. The next field has an area of 360 hectares. How many days will it take the tractor driver to plow it?
2. Round the given numbers to:
a) tens: 239; 452.
b) hundreds: 4 568; 12 782.
c) thousands: 9 546; 24 452.
3. Perform the operations.
| a) 14 956 – 5 694 : 3 – 8 405 = | b) (33 054 – 5 495) : 7 + 5 866 = |
4. Compare.
| a) 8 h 59 min … 530 min | b) $30 ha 83 m^2 … 3083 m^2$ |
5. Restore the digits where the asterisks are placed.
| ***** | 3 471 |
| – 576 | + **** |
| ——- | ——- |
| 5 843 | 33 083 |
Variant II.
1. Solve the problem.
A truck transported 720 tons of cargo in 8 days. It still needs to transport another 360 tons. How many days did it take to transport the entire cargo?
2. Round the given numbers to:
a) tens: 643; 359.
b) hundreds: 1 456; 16 341.
c) thousands: 9 215; 23 558.
3. Perform the operations.
| a) 7 924 – 5 832 : 2 – 3 822 = | b) (12 789 – 8 845) : 4 + 26 922 = |
4. Compare.
| a) 7 h 03 min … 703 min | b) $80 ha 456 m^2 … 80456 m^2$ |
5. Restore the digits where the asterisks are placed.
| ***** | 9 834 |
| – 953 | + **** |
| ——- | ——- |
| 9 778 | 13 854 |
Variant III.
1. Solve the problem.
A craftsman made 320 parts in 8 days. He still needs to make another 360 parts. How many days will it take him to make all the parts?
2. Round the given numbers to:
a) tens: 583; 362.
b) hundreds: 3 622; 14 999.
c) thousands: 6 356; 52 446.
3. Perform the operations.
| a) 8 573 – 4 422 : 2 – 1 567 = | b) ( 8 535 – 1 579 ) : 4 + 3 456 = |
4. Compare.
| a) 3 h 53 min … 243 min | b) $13 ha 34 m^2 … 13034 m^2$ |
5. Restore the digits where the asterisks are placed.
| ***** | 3 568 |
| – 457 | + **** |
| ——- | ——- |
| 9 223 | 13 569 |
Answers to Test No. 3 (2nd quarter)
Test No. 4
Variant I.
1. Perform the operations.
| a) 2455 * 2 = | b) 5676 * 3 = | c) 698 * 3 = | d) 2174 * 5 = |
2. Perform the operations.
| a) 1926 : 6 = | b) 2739 : 3 = | c) 5628 : 2 = | d) 5560 : 5 = |
3. Solve the equations.
| a) 5112 = Y : 6 | b) 1737 = X * 3 |
4. Solve the problem.
Misha jumped 4 m 5 cm. Kolya jumped 25 cm further. How far did Kolya jump?
Variant II.
1. Perform the operations.
| a) 5289 * 2 = | b) 9354 * 4 = | c) 528 * 6 = | d) 8734 * 5 = |
2. Perform the operations.
| a) 5370 : 6 = | b) 2568 : 3 = | c) 2232 : 4 = | d) 1290 : 5 = |
3. Solve the equations.
| a) 6118 = Y : 7 | b) 2940 = X * 4 |
4. Solve the problem.
Olya slept for 3 hours 45 minutes. Valya slept 35 minutes longer. How long did Valya sleep?
Variant III.
1. Perform the operations.
| a) 3321 * 2 = | b) 9298 * 3 = | c) 862 * 4 = | d) 3471 * 7 = |
2. Perform the operations.
| a) 5046 : 6 = | b) 2889 : 3 = | c) 2232 : 2 = | d) 3420 : 5 = |
3. Solve the equations.
| a) 3648 = Y : 8 | b) 1345 = X * 5 |
4. Solve the problem.
A craftsman made the first part in 1 hour 55 minutes. He worked 15 minutes longer on the second part. How much time did he spend making both parts?
Answers to Test No. 4 (2nd quarter)
Test No. 5
Variant I.
1. Solve the problems.
| a) 1,475 – 485 * 3 + 2,655 : 9 = | b) 3,648 : (5 – 3) + 356 * 4 = |
| c) 1,620 : 4 – 348 + 5 * 839 = | d) 6 * (202 – 76) + 5,523 : 7 = |
2. Solve the equations.
| a) X – 2,345 = 5 * 345 | b) 4,005 : 5 = Y + 800 |
3. Solve the problem.
In the workshop, 16 benches were made on Thursday, and on Friday, 5 more benches were made. It took 111 meters of boards to make all the benches. How many meters of boards were used on the second day?
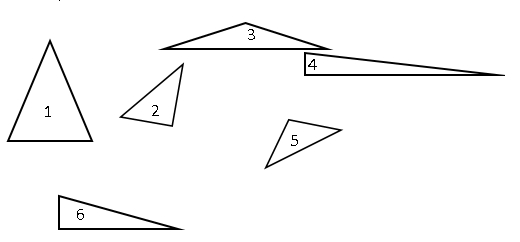
4. Look closely at the picture and write down:
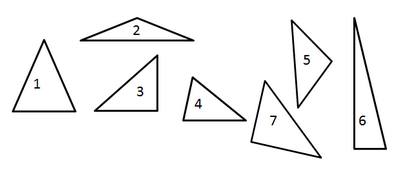
a) The numbers of rectangular triangles.
b) The numbers of obtuse-angled triangles.
c) The numbers of acute-angled triangles.
5. In the picture, three rectangles are depicted with their dimensions given. Calculate the perimeters and areas of the figures shown in the picture. Find the total area of all figures.
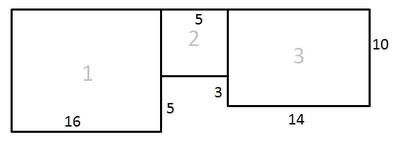
Variant II.
1. Solve the problems.
| a) 3,685 – 286 * 3 + 7,101 : 9 = | b) 1,548 : (9 – 3) + 983 * 4 = |
| c) 4,812 : 4 – 322 + 5 * 1,269 = | d) 7 * (459 – 276) + 3,199 : 7= |
2. Solve the equations.
| a) X + 1,574 = 6 * 289 | b) 4,109 : 7 = Y – 852 |
3. Solve the problem.
The master made 34 parts, and his apprentice made 12 parts less. It took 168 kg of material to make all the parts. How much material did the apprentice use?
4. Look closely at the picture and write down:
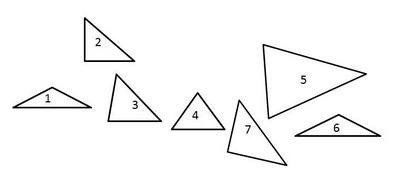
a) The numbers of rectangular triangles.
b) The numbers of obtuse-angled triangles.
c) The numbers of acute-angled triangles.
5. In the picture, three rectangles are depicted with their dimensions given. Calculate the perimeters and areas of the figures shown in the picture. Find the total area of all figures.
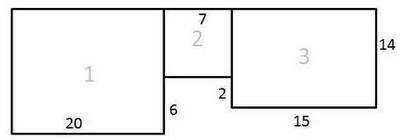
Variant III.
1. Solve the problems.
| a) 4,329 – 245 * 6 + 1,107 : 3 = | b) 4,401 : (2 + 7) + 419 * 5 = |
| c) 3,495 : 5 – 288 + 6 * 378 = | d) 5 * ( 302 – 176 ) + 5,706 : 6 = |
2. Solve the equations.
| a) X – 2,586 = 3 * 267 | b) 3,492 : 6 = Y – 2,560 |
3. Solve the problem.
On Tuesday, a tailor sewed 27 aprons, and on Wednesday, 8 more aprons were sewn. It took 124 meters of fabric to make all the aprons. How much fabric did the tailor use on Wednesday?
4. Look closely at the picture and write down:
a) The numbers of rectangular triangles.
b) The numbers of obtuse-angled triangles.
c) The numbers of acute-angled triangles.
5. In the picture, three rectangles are depicted with their dimensions given. Calculate the perimeters and areas of the figures shown in the picture. Find the total area of all figures.

Answers to Test No. 5 (3rd quarter)
Test No. 6
Variant I.
1. Solve the multiplication problems.
| a) 45 * 50 = | b) 380 * 24 |
| c) 473 * 30 = | d) 32 * 46 = |
2. Solve the division problems.
| a) 450 : 50 = | b) 360 : 90 = |
| c) 483 : 3 = | d) 138 : 46 = |
3. Solve the problem.
4200 notebooks were brought to school. All the notebooks were packed in packs of 60 each. On the first day, 20 packs were distributed. How many notebooks are left?
4. Solve the problem.
Two steamboats set off towards each other from two piers. The distance between the piers is 180 km. They met after 6 hours. At what speed was the second steamboat traveling if the speed of the first was 15 km/h?
5. Find the value of the expressions.
| a) (15,885 * 6 – 2,230 : 5) – 345 = | b) 62,697 – (2,449 * 7 + 4,524 : 3) = |
Variant II.
1. Solve the multiplication problems.
| a) 32 * 60 = | b) 145 * 24 |
| c) 276 * 70 = | d) 64 * 53 = |
2. Solve the division problems.
| a) 850 : 50 = | b) 640 : 80 = |
| c) 693 : 3 = | d) 230 : 46 = |
3. Solve the problem.
12,520 books need to be delivered to the city library. All the books are packed in boxes of 20 each. On the first day, 380 boxes were delivered. How many books are left to deliver?
4. Solve the problem.
From two settlements, two pedestrians set out towards each other. The distance between the settlements is 48 km. They met after 4 hours. At what speed was the first pedestrian walking if the speed of the second was seven km/h?
5. Find the value of the expressions.
| a) (1,845 * 6 – 240 : 3) – 345 = | b) 45,697 – (3,451 * 6 + 3,202 : 2) = |
Variant III.
1. Solve the multiplication problems.
| a) 47 * 80 = | b) 289 * 24 = |
| c) 288 * 20 = | d) 34 * 63 = |
2. Solve the division problems.
| a) 450 : 90 = | b) 360 : 30 = |
| c) 486 : 6 = | d) 625 : 25 = |
3. Solve the problem.
16780 kg of sugar were delivered to the warehouse. Then 52 bags of 40 kg each were taken away. How many kilograms of sugar are left in the warehouse?
4. Solve the problem.
From two cities, which are 630 km apart, 2 buses set off towards each other. They met after 7 hours. What is the speed of the first bus if the speed of the second bus is forty km/h?
5. Find the value of the expressions.
| a) (5672 * 5 – 2568 : 4) – 345 = | b) 23797 – (1 564 * 6 + 3 780 : 6) = |
Answers to Test No. 6 (3rd quarter)
Test No. 7
Variant I.
1. Solve the problems.
| a) 13087 : 23 = | b) 4005 : 89 = |
| c) 143 * 231 = | d) 302 * 563 = |
2. Compare the magnitudes.
| a) 560 dm … 65 m | b) 3 t 602 kg … 3206 kg |
3. Solve the problem.
Apples were brought to the store and placed in 21 boxes. Each box holds 12 kg. How many boxes are needed to hold 18 kg of apples each?
4. Restore the missing digits.
| **** | *** |
| * 3 | * 6 |
| ——- | ——- |
| 9 777 | 2 850 |
Variant II.
1. Solve the problems.
| a) 10032 : 22 = | b) 2376 : 27 = |
| c) 341 * 834 = | d) 563 * 123 = |
2. Compare the magnitudes.
| a) 56 m … 650 dm | b) 12 t 702 kg … 12720 kg |
3. Solve the problem.
There are 22 chairs in each row, and there are a total of 16 such rows in the hall. How many rows will the same number of chairs take if each row is arranged with 11 chairs?
4. Restore the missing digits.
| **** | *** |
| * 7 | * 8 |
| ——- | ——- |
| 7 630 | 5 456 |
Variant III.
1. Solve the problems.
| a) 44184 : 56 = | b) 39483 : 41 = |
| c) 617 * 234 = | d) 324 * 933 = |
2. Compare the magnitudes.
| a) 12 m 6 dm … 1260 cm | b) 18 t 892 kg … 18829 kg |
3. Solve the problem.
There are 18 chairs in each row, and there are a total of 15 such rows in the hall. How many rows will the same number of chairs take if each row is arranged with 30 chairs?
4. Restore the missing digits.
| *** | *** |
| * 9 | * 5 |
| ——- | ——- |
| 7 101 | 905 |
Answers to Test No. 7 (4th quarter)
Test No. 8
Variant I.
1. Solve the problems.
| a) 2,485 + 5,059 = | b) 32,495 + 948 = | c) 32,945 – 5,473 = | d) 3,595 – 294 = |
| e) 286 * 26 = | f) 625 * 125 = | g) 10,396 : 23 = | h) 335,808 : 636 = |
2. Find the values of the expressions.
| a) 320 : 80 * 810 : 90 = | b) (12,394 + 45,394) : 2 – 23 * 46 = |
3. Solve the problem.
A car and a cyclist set off from the bus station in opposite directions. The car’s speed is 70 km/h, and the cyclist’s speed is 23 km/h. What will be the distance between them after 2 hours?
Variant II.
1. Solve the problems.
| a) 2,449 + 9,512 = | b) 28,561 + 988 = | c) 12,945 – 4,677 = | d) 3,461 – 998 = |
| e) 179 * 68 = | f) 879 * 351 = | g) 203,305 : 365 = | h) 37,422 : 54 = |
2. Find the values of the expressions.
| a) 560 : 70 + 320 : 80 = | b) (12,299 – 2,395) : 2 – 29 * 88 = |
3. Solve the problem.
A car and a bus set off from two cities towards each other at the same time. The car’s speed is 70 km/h, and the bus’s speed is 65 km/h. What is the distance between the cities if the car and the bus met after two hours?
Variant III.
1. Solve the problems.
| a) 6,450 + 9,283 = | b) 26,172 + 623 = | c) 28,765 – 5,499 = | d) 3,897 – 995 = |
| e) 233 * 76 = | f) 834 * 889 = | g) 43,776 : 96 = | h) 120,482 : 214 = |
2. Find the values of the expressions.
| a) 34 + 810 : 90 + 4 * 16 = | b) 34 * 12 + (7,923 – 1,395) : 2 = |
3. Solve the problem.
A car and a cyclist set off in one direction at the same time. The car’s speed is 56 km/h, and the cyclist’s speed is 19 km/h. What will be the distance between them after 2 hours?
Answers to Test No. 8 (4th quarter)
Materials for preparation for control works. Review of the material covered last year. With solutions.
1. Mom had x rubles. According to the problem, she spent 1,894 rubles, and she had 2,589 rubles left. Therefore, you can write the equation: x – 1894 = 2589. Solve the equation: x = 1894 + 2589 = 4483. Answer: Mom had 4483 rubles.
2. Let there be x costumes in the store. According to the problem, when 148 costumes were sold, there were 48 left. Therefore, you can write the equation: x – 148 = 48. Solve the equation: x = 148 + 48 = 196. Answer: there were 196 costumes in the store.
3. Let x be the weight of oranges in one box. According to the problem, when 6 boxes were sold, there were 56 kg left. Therefore, you can write the equation: x * 6 = 56. Solve the equation: x = 56 / 6 = 9.33 (round to the nearest whole number). Answer: there were about 9 kg of oranges in one box.
4. According to the problem, there were 30 liters of milk in one can, and in 5 pitchers – 10 liters. Let’s find out how much milk is in one pitcher: 10 liters / 5 = 2 liters. Thus, there is less milk in one pitcher than in two cans 30 / 2 = 15 times.
5. Let x be the amount of potatoes harvested from the second field. According to the problem, 30 tons of potatoes were harvested from the first field, and from the second field – twice less. That is, x = 30 / 2 = 15 tons of potatoes. The total amount of potatoes is 30 + 15 = 45 tons. Let’s distribute it equally into 5 boxes: 45 tons / 5 = 9 tons. Answer: each box contains 9 tons of potatoes.
6. Let the number of children who rested in August be x. According to the problem, 264 children rested in June, and in July there were 37 more. That is, in July, 264 + 37 = 301 children rested. The total number of children who rested in the camp is 1000 (for three months). Therefore, you can write the equation: 264 + 301 + x = 1000. Solve the equation: x = 1000 – 264 – 301 = 435. Answer: 435 children rested in August.
7. Let the first brigade repair x km of road in 1 day. According to the problem, the second brigade repaired 100 meters more in 1 day. That is, the second brigade repaired x + 100 meters of road. The total revenue of both brigades in 1 day is (1 km 100 m + 1 km 200 m) = 2 km 300 m = 2.3 km. Therefore, you can write the equation: x + (x + 100) = 2.3. Solve the equation: 2x + 100 = 2.3. 2x = 2.3 – 100 = -97.7. It is impossible to calculate the quantity of something, since the obtained value is negative. It is necessary to check the problem statement or the problem statement is incorrect.
8. Let the cost of one costume be x rubles. According to the problem, they bought 8 dresses for 1850 rubles each and 12 costumes. They paid 340,000 rubles for the entire purchase. Therefore, you can write the equation: 8 * 1850 + 12 * x = 340,000. Solve the equation: 14,800 + 12x = 340,000. 12x = 340,000 – 14,800 = 325,200. x = 27100 / 12 = 2266.67 (round to the nearest whole number). Answer: the cost of one costume is about 2267 rubles.
9. Let the cost of one pair of chairs be x rubles. According to the problem, the sofa is twice as expensive, and the mirror is twice as expensive as the sofa and pair of chairs. That is, the mirror costs 2 * (2 * x) = 4 * x rubles. The total amount of all purchases is x + 2 * x + 4 * x = 7 * x. If the total amount of purchases is 3400 rubles, then 7 * x = 3400. Solve the equation: x = 3400 / 7 = 485.71 (round to the nearest whole number). Answer: the mirror cost about 485 rubles.
10. Let the number of bells be x. According to the problem, the number of flowers is three times the number of bells, and the number of balls is four times the number of flowers. That is, the number of flowers is 3 * x, and the number of balls is 4 * (3 * x) = 12 * x. Then the total number of items purchased is x + 3 * x + 12 * x = 16 * x. If the total number of items is 51, then 16 * x = 51. Solve the equation: x = 51 / 16 = 3.19 (round to the nearest whole number). Answer: bought about 3 balls.
11. Let the revenue for the first day be x rubles. According to the problem, the revenue for the second day is 280 rubles more, and the revenue for the third day is twice less than the sum of the revenue for the first and second days. That is, the revenue for the second day is x + 280 rubles, and the revenue for the third day is 2 * (x + x + 280) = 4 * (x + 280) rubles. The total revenue for all three days is x + (x + 280) + 4 * (x + 280) = 6 * x + 1960 rubles. If the total revenue for all three days is 1960 rubles, then 6 * x + 1960 = 1960. Solve the equation: 6 * x = 1960 – 1960 = 0. It is impossible to calculate the revenue on the third day, since the obtained value is zero.
Materials for preparation for control works. Solution of problems on speed, time, and distance.
46. Two tourists walked at a snail’s pace and covered a funny 36 micrometers. How many hours did it take them?
47. We traveled from the dacha to the house in a blink for 2 hours at the speed of a supersonic bus. How far is our dacha from the city?
48. The heart beats 12,000 times in a day. With what funny speed does the heart beat (beats per hour)?
49. Two cars set off from the city in opposite directions at the same time. The speed of the first is equal to the speed of a tortoise, and the speed of the second is 20 km/h more. What will be the distance between them in 5 hours?
50. A cyclist rode from the city to the village in 4 hours at a snail’s pace. At what speed did he ride back if it took him 6 hours for the round trip?
51. Tourists traveled 265 km. For 3 hours, they drove by car at a speed of 15 km/h. The rest of the way, they traveled on horses at a speed of 1 km/h. How many hours did they ride on horses?
52. Two pedestrians simultaneously set out from two cities towards each other. The first walked at the speed of a running tortoise, and the second at the same speed. They were on the way for 3 hours before meeting. What is the distance between the cities?
53. Two cyclists set off in opposite directions from the city at the same time. What will be the distance between them after 4 hours if the speed of the first is 180 km/h and the speed of the second is 240 km/h?
54. The distance between two cities is 1000 km. A car travels it in 5 hours, and a bus in 20 hours. In how many funny hours will they meet if they set off at the same time towards each other?
55. A tourist covered 250 km in 3 days. On the first day, he sailed on a boat at a speed of 14 m/h for 8 hours, on the second day, he rode a motorcycle for 2 hours at a speed of 50 m/h. The remaining distance on the third day, he covered by running. How many meters did the tourist run?
56. Two settlements, the distance between which is 81 km, simultaneously set off towards each other two pedestrians. One of them walked at a speed of 6 m/h, and the other at 1 m/h less. What will be the distance between them after 7 hours?
Materials for preparation for control works. Problems on finding the perimeter, area, and sides of geometric figures.
84. Draw a square with a side of 8 cm and find its perimeter.
85. Draw a rectangle with sides of 4 cm and 9 cm. Find its perimeter.
86. The area of a rectangle is 68 cm2. Find the width if its length is 17 cm.
87. The side of a square is 18 cm. Find the perimeter and area.
88. The area of a rectangle is 56 cm2. The width is 7 cm. Find the length of the rectangle.
89. The perimeter of a rectangle is 100 cm. Its length is 10 cm. Find the width.
90. The side of a square is 5 cm. Find its perimeter and area.
91. The perimeter of a square is 40 cm. Find its side.
92. The perimeter of a rectangle is 16 cm, and the length is 4 cm. Find the width of the rectangle and make a drawing.
93. The perimeter of a rectangle is 56 cm. The width is 7 cm. Find the length.
94. The perimeter of a rectangle is 40 cm. The length is 10 cm. Find the area of the rectangle.
95. The perimeter of a square is 48 cm. Find the side.
96. The side of a square is 12 cm. Find the perimeter and area.
97. Draw a square with a perimeter of 8 cm.
98. Draw a rectangle with a perimeter of 10 cm, and one of the sides is 1 cm.
99. The length of a rectangle is 6 cm, and the width is twice as much. Find the perimeter and area of the rectangle.
100. Find the perimeter of a rectangle if one side is 4 cm, and the other is 3 times more. Make a drawing.
101. Draw a rectangle with a width of 2 cm and a length 4 times less. Find its perimeter.
102. The perimeter of a square is 8 cm. Find the area of the square.
103. The area of a rectangle is 8 cm2, and the width is 2 cm. Find the area.
104. The area of a rectangular flower bed is 48 m2. What could be its length and width?
105. It is necessary to make frames of rectangular shape from wire. The sides of the frame are 20 and 10 cm. How much wire will be needed to make three such frames?
Materials for preparation for control works
1. Write down the numbers that contain:
| 9 | hundreds | 1 | tens | 2 | ones | = _____ | 0 | hundreds | 6 | tens | 6 | ones | = _____ | |
| 8 | hundreds | 8 | tens | 8 | ones | = _____ | 1 | hundreds | 9 | tens | 5 | ones | = _____ | |
| 6 | hundreds | 9 | tens | 2 | ones | = _____ | 4 | hundreds | 8 | tens | 6 | ones | = _____ | |
Fill in the table
| Addend | 284 | 702 | 407 | 194 | 118 | ||
| Addend | 309 | 559 | 160 | 459 | |||
| Sum | 989 | 660 | 1000 | 695 | 786 |
Fill in the table
| Subtrahend | 141 | 329 | 655 | ||||
| Subtract | 326 | 105 | 125 | 209 | |||
| Difference | 559 | 963 | 862 | 440 | 756 | 732 | 978 |
4. Fill in the table.
| e | 322 | 350 | 354 | 308 | 368 | 355 | 343 |
| e-90 | … | … | … | … | … | … | … |
| f | 443 | 443 | 453 | 433 | 423 | 463 | 473 |
| f+80 | … | … | … | … | … | … | … |

Leave a Reply