Math textbook for second grade.
Hundred. Addition and subtraction
1. Read the numbers: 15, 38, 42, 24, 83. How many units are there in the first and second digits of each? Replace each number with the sum of its digit components.
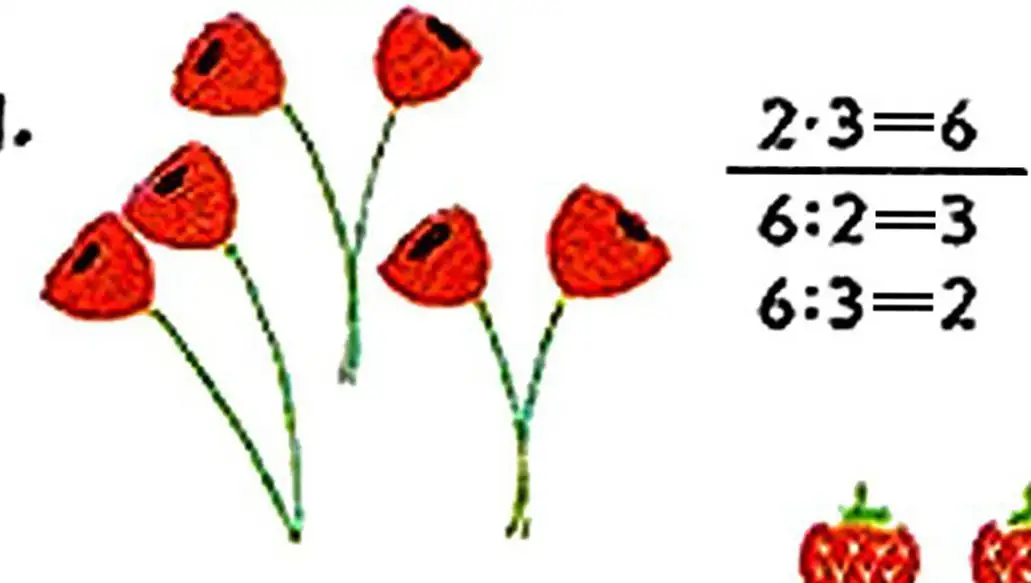
2. Read the numbers: 7, 2, 22, 77, 27, 72. Which digits are used to write these numbers? Write these numbers in decreasing order.
3. Write four different two-digit numbers using the digits 3 and 5. Write them in increasing order.
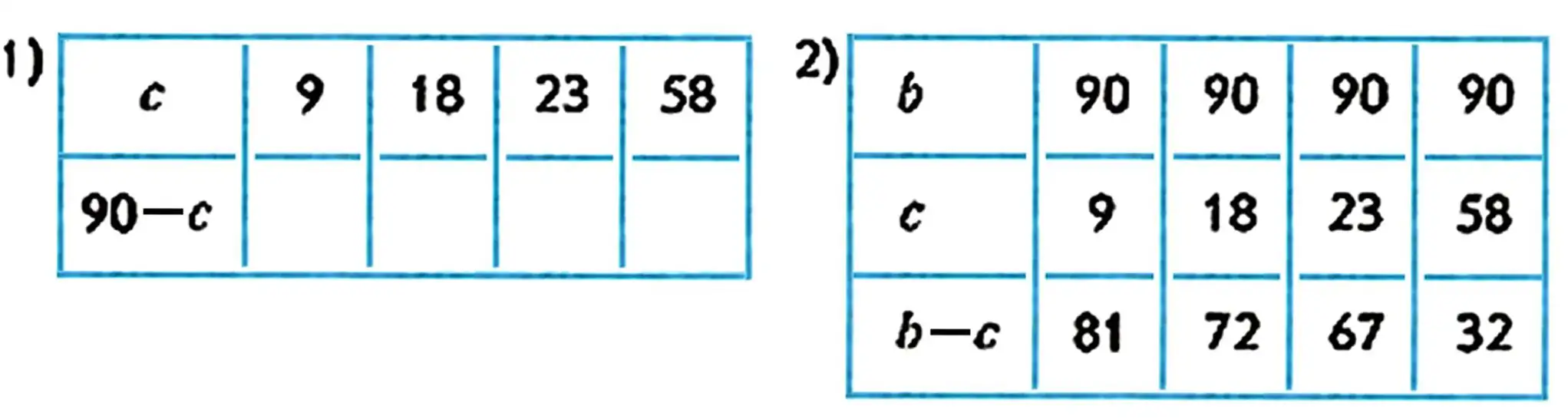
| 4. 67+1 | 50+8 | 30+40 | 79+1 | (7+3)+6 |
| 67-1 | 9+70 | 60-50 | 57-7 | (6+2)-7 |
| 19+1 | 26-6 | 40+60 | 2+90 | 4+(9+1) |
| 80-1 | 26-20 | 100-20 | 69-60 | 10-3+4) |
5. Students were supposed to dig a bed 23 meters long, but they dug 3 meters less. How many meters of the bed did the students dig?
6. Pioneers helped the collective farm in harvesting potatoes. On the first day, they collected 40 baskets of potatoes, and on the second day, 10 baskets more. How many baskets of potatoes did the pioneers collect on the second day? In two days?

7. 10 potato diggers worked in the potato field, and there were 4 fewer trucks than diggers. How many trucks worked in the potato field?
8. Solve the examples using a convenient method:
(10+6)+3 (30+4)4-20 (60+2)+8 (3+7)+5
(10+6)-3 (30+4)-20 (40+10)—6 (4+4)-6
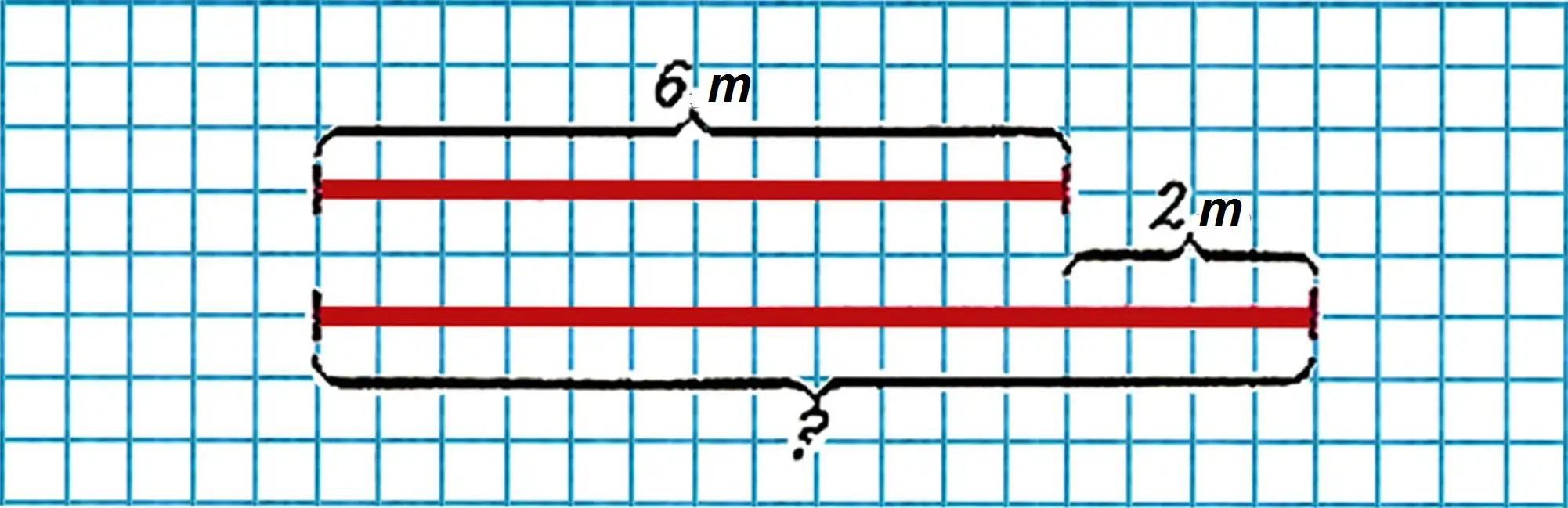
9. Vanya had two pieces of wire: one 6 meters long, and the other 2 meters longer. How long was the second piece of wire?
You can express this problem as a drawing, taking one division as 1 meter,
10. From one apple tree, they picked 20 baskets of apples, and from another tree, 10 baskets less. How many baskets of apples did they pick from two apple trees?
Express the condition of this problem as a drawing, taking one cell as 1 basket.
11. Draw a segment 4 cm long, increase it by 6 cm. What length will the segment be?
12. Draw two segments: the length of the first is 1 dm 4 cm, and the second is 6 cm shorter. What is the length of the second segment?
13. 
| (40+6)—3 | 15-10+30 | 49+1-30 | 5+4-9 |
| (10+5)+5 | 60+9-1 | 90-1-9 | 8-6-2 |
| (60+10)—2 | 78-8+20 | 99+1-40 | 8-8+6 |
15. Solve the examples with an explanation:
| 25+4 | 49-7 | 54+20 | 73-20 | 80-4 |
| 16.16+3 | 23+7 | 15-4 | 40-9 | 60-1 |
| 16+30 | 66+4 | 28+50 | 13+7 | 90+3 |
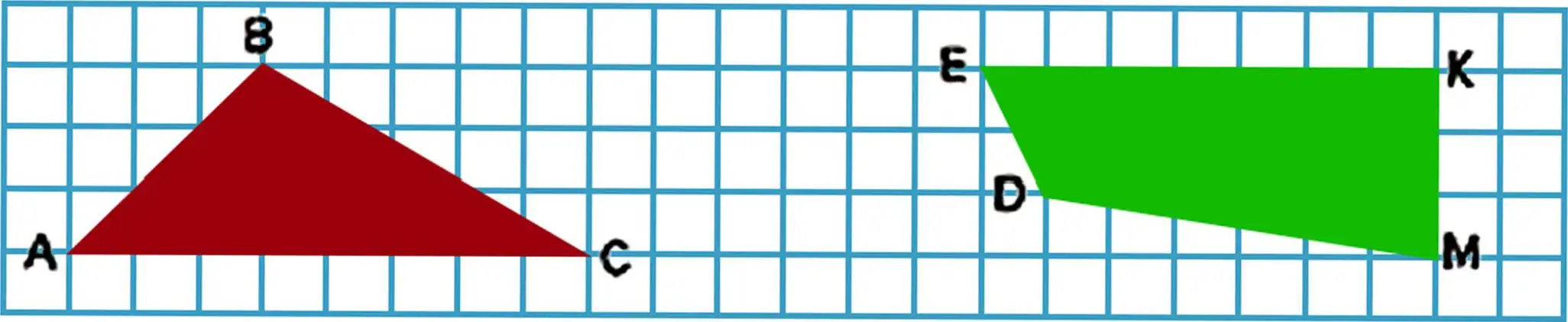
| 48-30 | 20-5 | 96-70 | 14+60 | 89+1 |
17. Yura and Volodya went to the forest for mushrooms. Yura found 16 white mushrooms, and Volodya found 6 fewer mushrooms than Yura. How many mushrooms did the boys find together?
Represent the condition of this problem as a drawing, taking one cell as 1 mushroom.
18. There were 32 books on one shelf in the library, and 40 books on another shelf. 20 books were given to the children. How many books are left? Solve the problem in different ways.
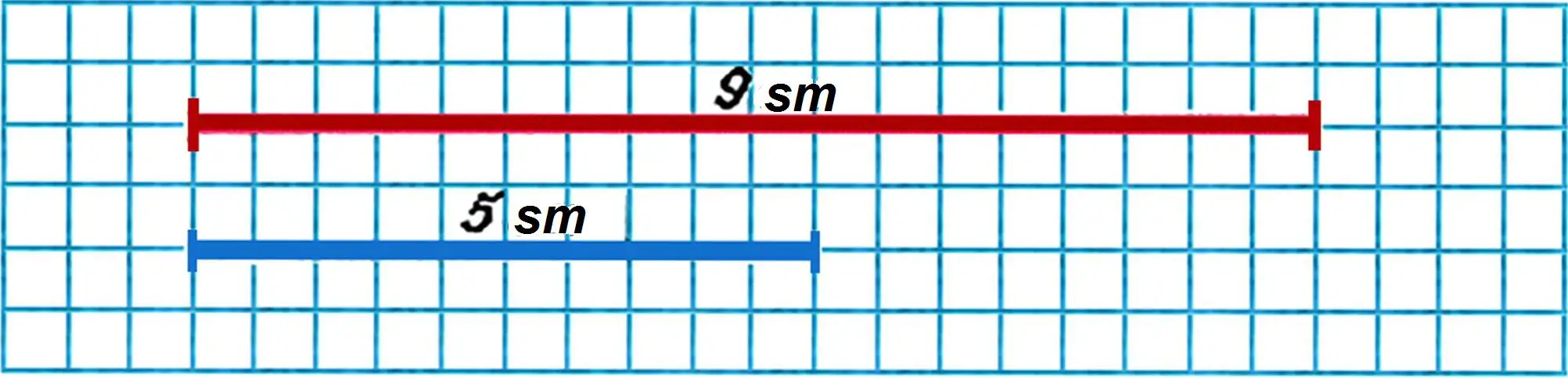
19. By how many centimeters is the blue segment shorter than the red one?
20. A segment 12 cm long was reduced by 10 cm. What is the length of the resulting segment?
21. Choose such numbers that the statements are true:
___ < 7 3+ ___ < 6 10- ___ > 4
22. 52+8 19+1 10+54 40+40
23. 1) Look at the picture and explain how the examples are composed:
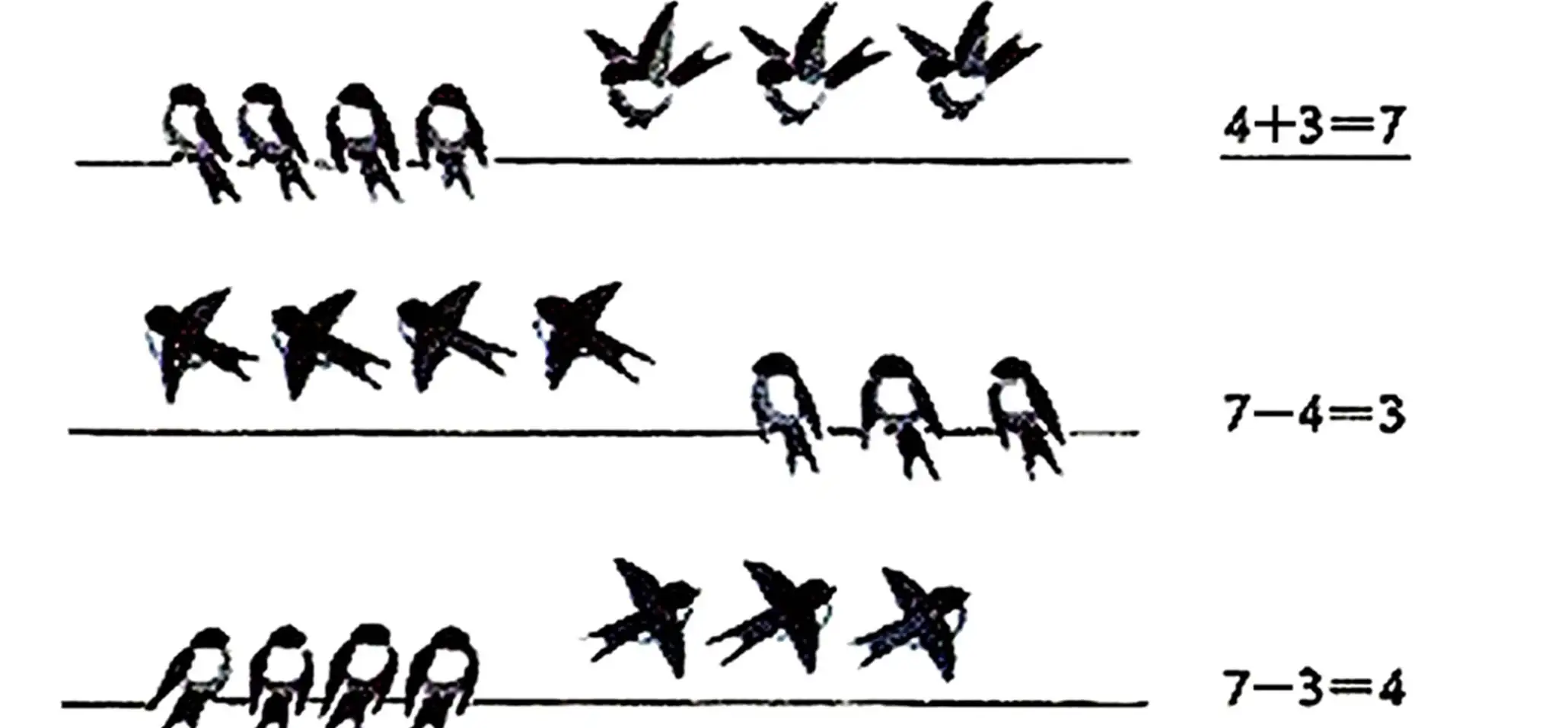
2) Solve the examples and compare in each column the second and third examples with the first one. How did you get the second addend? The first addend?
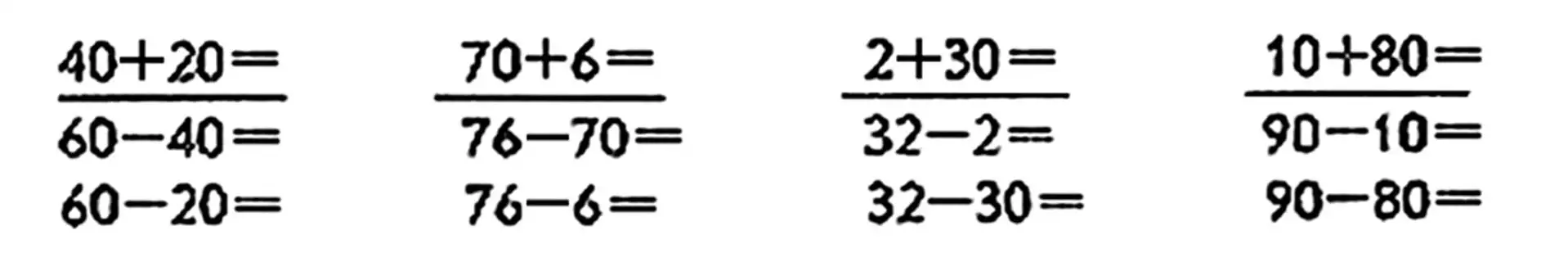
24. x+4=16 7+х=48 & x+1=18 6+х=30
25. There were 48 men and 30 women working in the workshop. Another 10 workers arrived. How many workers are there in the workshop now?
26. Compose problems for their solution:
1) 32- 2 2) 24+6 3) 24+(24+6
27. Are the following records correct?
32+40<32+60 87-5 87-3 94-50 94-30 48-20 38-20 61+5 64+5 27+30 27+3
28. 6+74-8 62-20+4 2+38 8 dm = __ cm
80-6+20 57+3-6 7+91 5 m = __ dm
29. Examine the picture and identify the names of these shapes. Find rectangles among the quadrilaterals. Find squares among the rectangles.
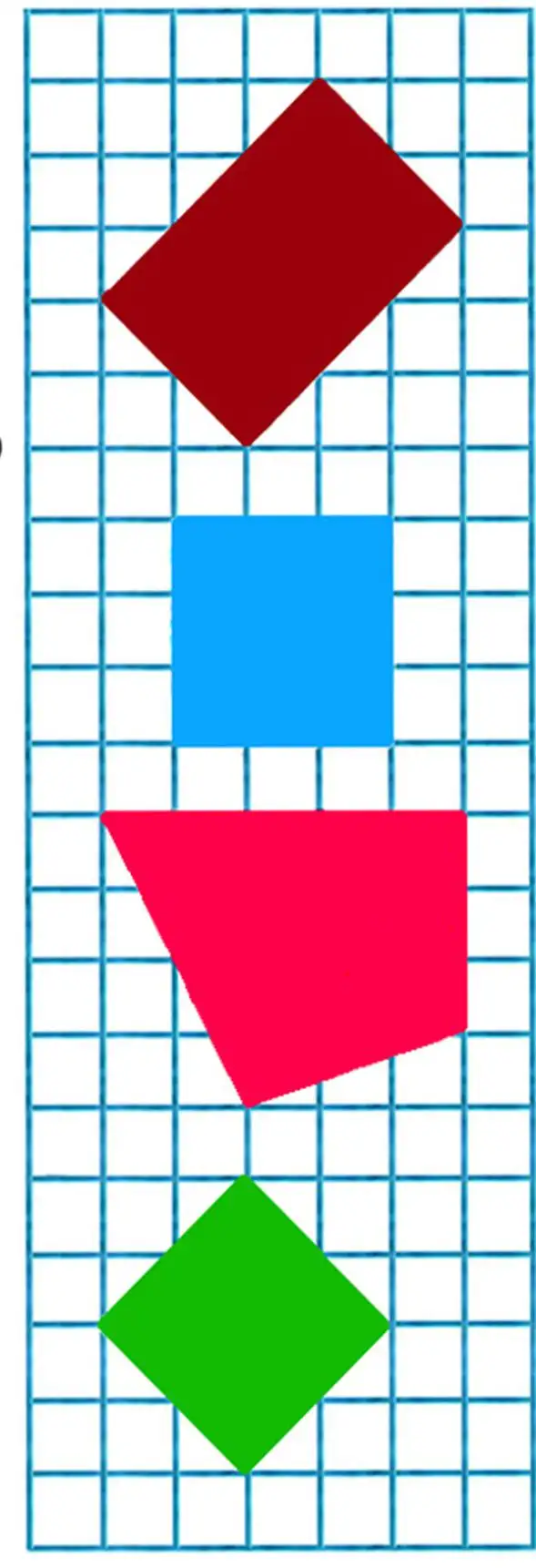
Mathematical Expressions.
30. 17 + 3 12 – 8
The sum of the numbers 17 and 3. The difference between the numbers 12 and 8.
These are mathematical expressions or, in short, expressions.
17 + 3 = 20, 12 – 8 = 4.
20 is the value of the first expression;
4 is the value of the second expression.
Read the expressions and find their values:
90-4 38+20 61-50 8+42 19-7
31. Create a problem based on the picture:
Let’s denote the number of pencils in the second box by the letter x. Formulate an equation based on the problem: 6+x=10. Solve the equation.
32. Solve the problems by forming equations:
1) There were 7 tracked tractors and several wheeled tractors in the field, a total of 10 tractors. How many wheeled tractors were working in the field?
2) 50 boxes of grapes were loaded onto two trucks. 30 boxes were loaded onto one of them. How many boxes were loaded onto the other truck?
33. Choose numbers so that the statements are true:

34. In a sports club, 10 girls were engaged, and there were 2 fewer boys than girls. How many children were engaged in the sports club in total? Represent the condition of this problem as a drawing.
| 26+4 | 68-2 | 32+6 | 84-20 | 15-15 |
| 26+10 | 68-6 | 32+8 | 30-20 | 19+0 |
| 26+20 | 68-20 | 32+10 | 75-20 | 27-0 |
36. Solve the examples using a convenient method:
8+(2+4) 9+(1+6) 16+(4+3) 20+(10+4)
15—(5+1) 12—(2+7) 32-(2+5) 40-(20+3)
| Summand | 3 | 6 | 9 | |||
| Summand | 10 | 20 | 30 | |||
| Sum | 20 | 27 | 30 | 38 | 40 | 46 |
38. Write down mathematical expressions and find their values: 1) The difference between the numbers 20 and 7; 44 and 30; 97 and 90.
2) The sum of the numbers 9 and 41; 15 and 50; 24 and 6.
39. A barrel of honey weighs 58 kg. An empty barrel weighs 8 kg. How many kilograms does the honey weigh?
40. Create a problem based on the brief recording and solve it in different ways:
41. Olya raised 25 chicks over the summer, and her sister raised 20 chicks. How many more chicks did Olya raise than her sister?
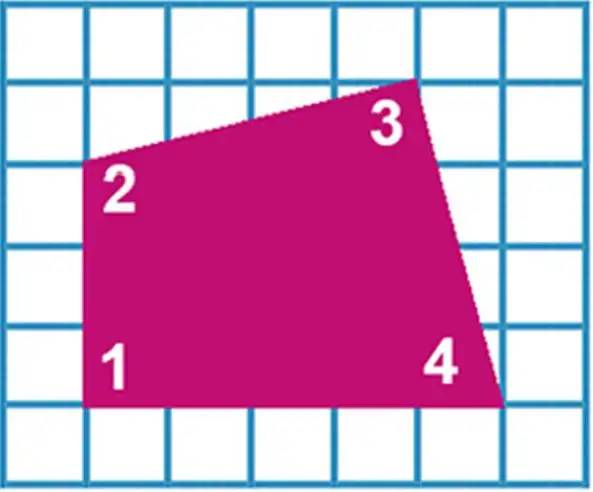
42. Find right angles in the quadrilateral and list their numbers.
43. 9+31 58+30-20 90 m = ___ cm
3+46 41+9-7 40 cm = __ dm
Addition Check.
There were 10, and 7 were taken. How many are left?
44. To check addition, subtract one of the addends from the sum. If the solution is correct, the other addend will be obtained.
57 + 12=69 Check: 69-57 = 12
Solve examples with verification: 35+24 9+17
45. Solve examples with explanation: 7+5 38+4 13—5
| 8+6 | 27+7 | 12-8 | 34-8 | 22-7 |
| 7+4 | 38+6 | 13-7 | 56-9 | 56+6 |
47. Write down all single-digit numbers in ascending order. Increase each of them by 8.
48. 1) Arrange 7 circles in a row, with 2 circles less in the first row than in the second. How many circles are in the second row?
2) Draw two line segments: the length of the first one is 6 cm, it is 2 cm longer than the second one. What is the length of the second line segment?
49. In mathematics, Latin letters are used to denote unknown numbers, for example, x. Also, remember four letters: Aa, Bb, Cc, Dd.
50. a+8=12 4+6 = 15 c+7 = 20
51. In a barrel, there were 40 buckets of water. In the morning, 12 buckets were taken for watering flowers, and in the evening, 15 buckets were taken. How many buckets of water are left in the barrel? Solve the problem in different ways.
52.
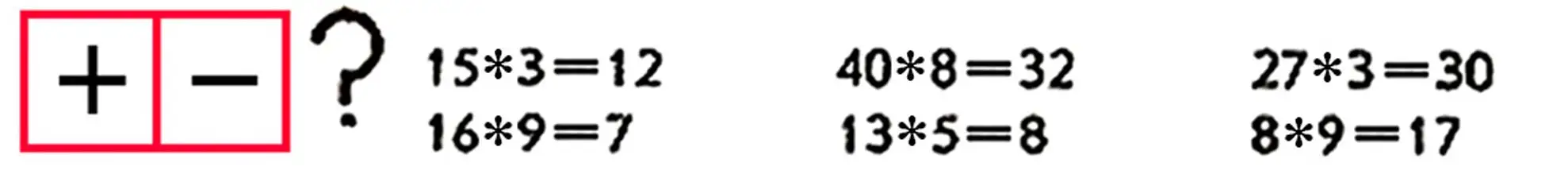
| 29-17 32-8 30-5 9+7
10+18 67+7 30-15 18-9 80-67 35-9 67-3 3+8 62+26 16+5 60-13 14-6 |
54. Nina found 23 acorns. Katya found 6 more acorns than Nina, and Olga found 9 fewer acorns than Katya. How many acorns did Olga find?
55. 1) From the first beehive, 25 kg of honey were taken, and from the second one, 5 kg more than from the first. How many kilograms of honey
were taken from the second beehive?
2) From the first beehive, 25 kg of honey were taken, 5 kg more than from the second one. How many kilograms of honey were taken from the second beehive?
| Minuend | 50 | 50 | 50 | 50 | 50 | 50 |
| Subtrahend | 3 | 10 | 14 | 35 | 48 | 50 |
| Difference |
57. Write down the expressions and calculate their values:
1) Subtract the sum of 10 and 3 from 35.
2) Add the sum of 20 and 4 to 56.
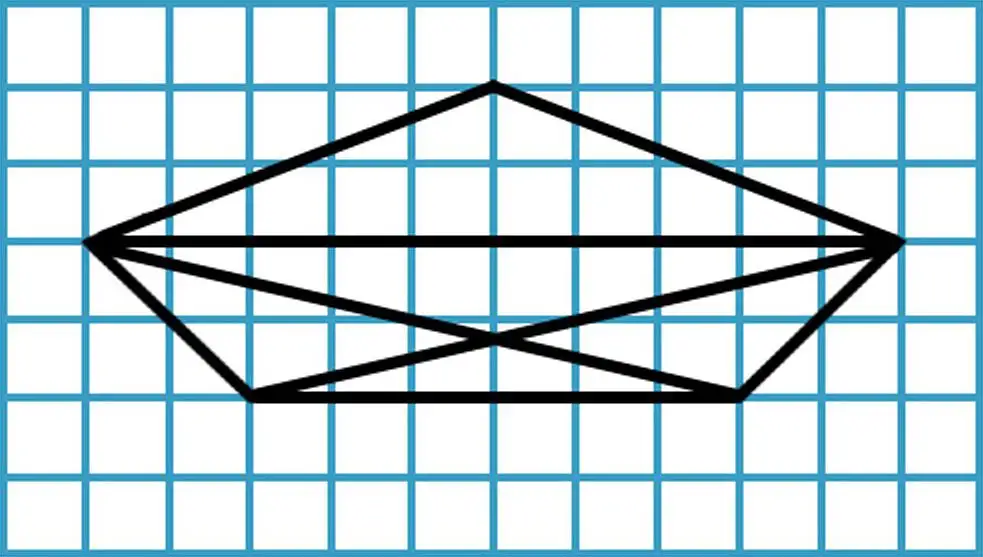
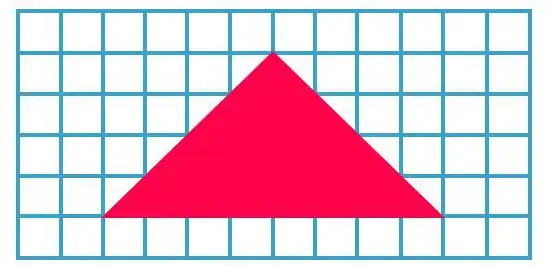
58. How many triangles are there in this diagram?
59. 6-2=4 
4+2=6 
6 — minuend, 2 — subtrahend, 4 — difference.
Explain how the minuend and subtrahend are obtained.
| Minuend | 24 | 37 | 45 | |||
| Subtrahend | 4 | 18 | 32 | |||
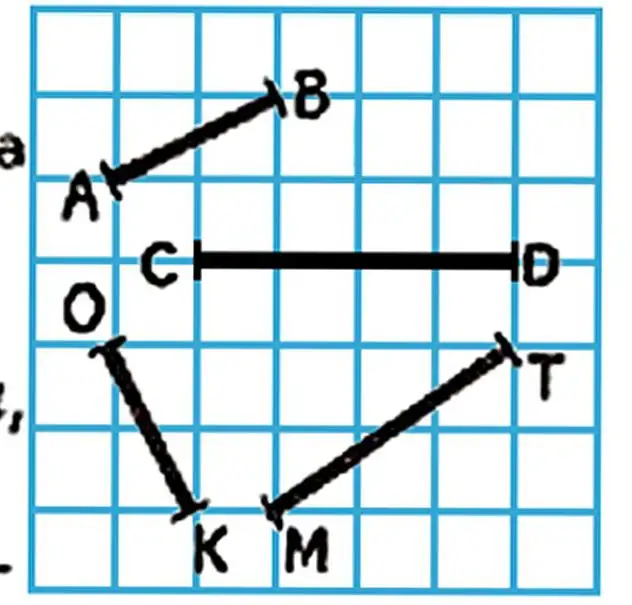
| Difference | 16 | 13 | 12 | 11 | 6 | 0 |
61. Solve equations: C—8=14 20—x=7 48—x=17 b—24=9
62. The Young
Pioneers planted 40 strawberry bushes in the first row, 6 bushes fewer in the second row than in the first, and 10 bushes more in the third row than in the second. How many strawberry bushes did the Young Pioneers plant in the third row?
63. Insert the operation signs instead of asterisks to make the expressions correct.
| 60*7=53 | 49*18=31 | 26*42=68 | 31*4=27 |
| 16*7=23 | 67*23=90 | 90*68=22 | 5*27=32 |
| 32*8=24 | 70*24=46 | 50*35=85 | 40*6=34 |

64. There were a total of 20 cranes on the construction site. Then 4 large cranes and 6 small cranes were transferred to another construction site. How many cranes are left on the construction site?
65. Create problems based on the given expressions:
1) 12-7 2) 12+(12-7)
66. Draw a rectangle with sides of 4 cm and 2 cm.
Subtraction Verification.
67. To check subtraction, add the subtrahend to the difference. If the solution is correct, the minuend will be obtained-
53—8 = 45 Verification: 45+8=53
Subtraction can also be checked by subtracting the difference from the minuend. If the solution is correct, the subtrahend will be obtained.
78—27 = 51 Verification: 78—51=27
Solve with verification: 96—75, 32—8
68. Solve the problems by forming equations:
1) There were 18 roses in the bouquet. Some roses were given away. There were 8 roses left. How many roses were given away?
2) After cutting 3 liters of fabric from a piece, there were still 10 meters left in it. How many meters of fabric were in the piece originally?
3) From which number do you need to subtract 9 to get 20?
4) The minuend is 16, the subtrahend is unknown, and the difference is 10. Find the subtrahend.
69. In the first skein, there are 28 threads, in the second one, 30 /4, and in the third one, 5 threads less than in the first and second ones together. How many threads are there in the third skein?
70. Compare the numbers and say how much the first one is greater or less than the second: 82 and 50, 14 and 27, 3 and 51.
71. 54-31 18+7 6+16 6+6+6+6+6
45+15 35-9 8+38 7+7+7+7+7
60-52 42-8 7+47 3+8+8+8+8
72. Memorize four more Latin letters: Mm, Nn, Pp, Rr.
73. Solve the examples with explanations:
| 37+48 | 73-25 | |
| 74. 38+14 | 15+7-14 | 40 cm = □ dm |
| 51-12 | 60-34+8 | 6 dm = □ cm |
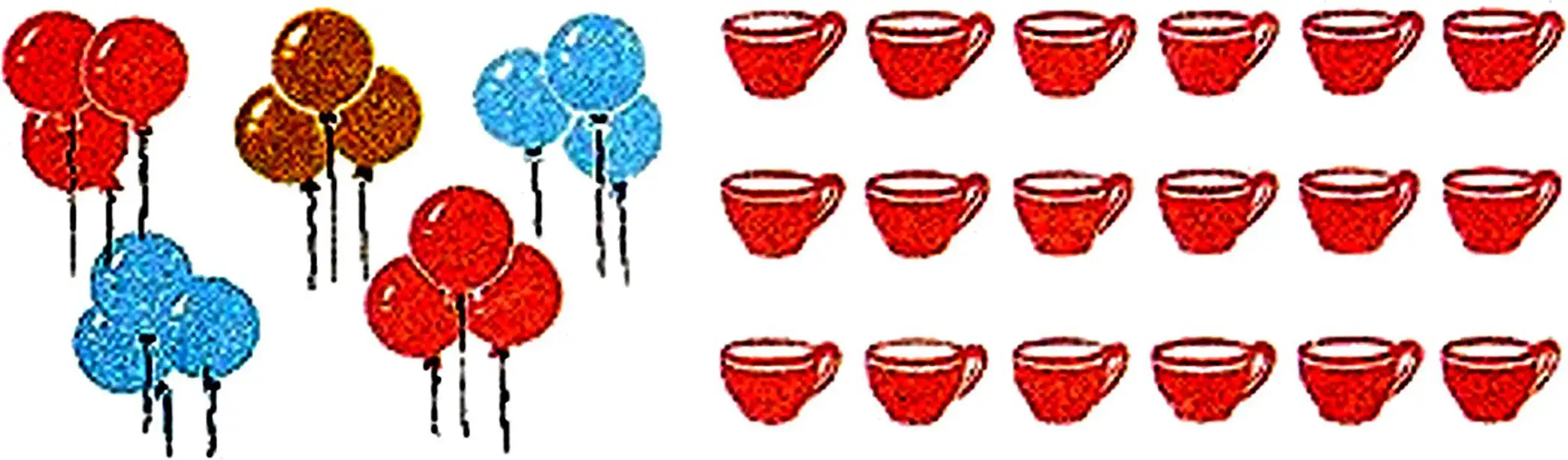
| 26+26 | 74+9-27 | 80 dm = □ m |
| 34-17 | 83-5+12 | 9 m: = □ dm |
75. A chair costs 25 rubles, a chair is 5 rubles, and a table is 10 rubles more than the chair and the chair together. How much does the table cost?
76. Create problems with equations:
1) 6—12=35 2) 54-х=18
78. Write expressions and find their values:
1) Add the sum of 18 and 2 to the sum of 6 and 4.
2) Subtract the sum of 35 and 5 from the sum of 9 and 1.
79. Pick numbers so that the statements are true:
1) ___ – 4>6 2) ___ – 4<6
80. The teacher handed out 8 notebooks evenly to two students. How many notebooks did each student receive?
81. The teacher handed out 6 notebooks, 2 to each student. How many students received notebooks?
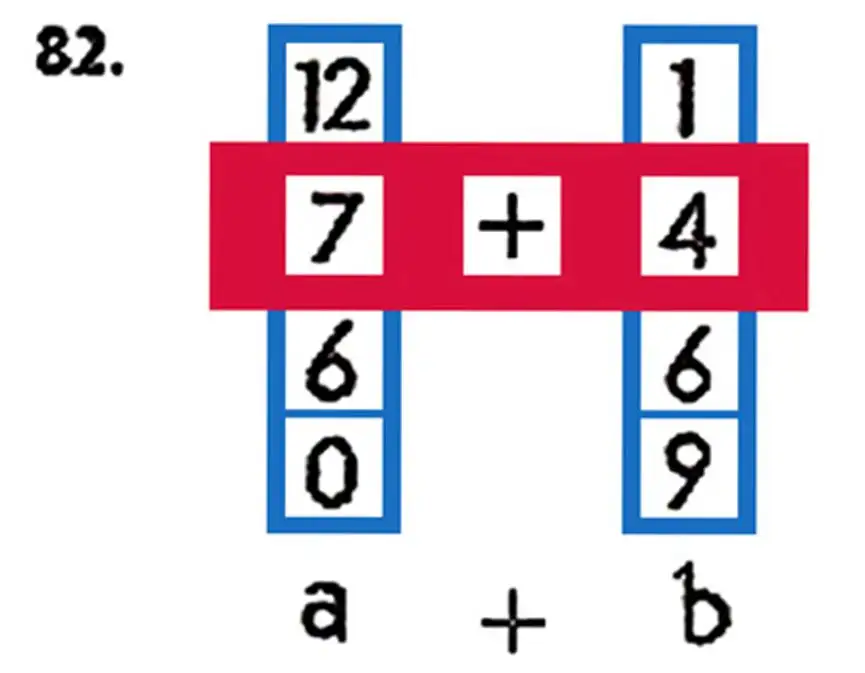
a — any number that can be the first summand;
b — any number that can be the second summand;
a + b — the sum of numbers a and b;
7, 12, 6, 0, … — numerical values of the letter a;
4, 1, 6, 9, … — numerical values of the letter b.
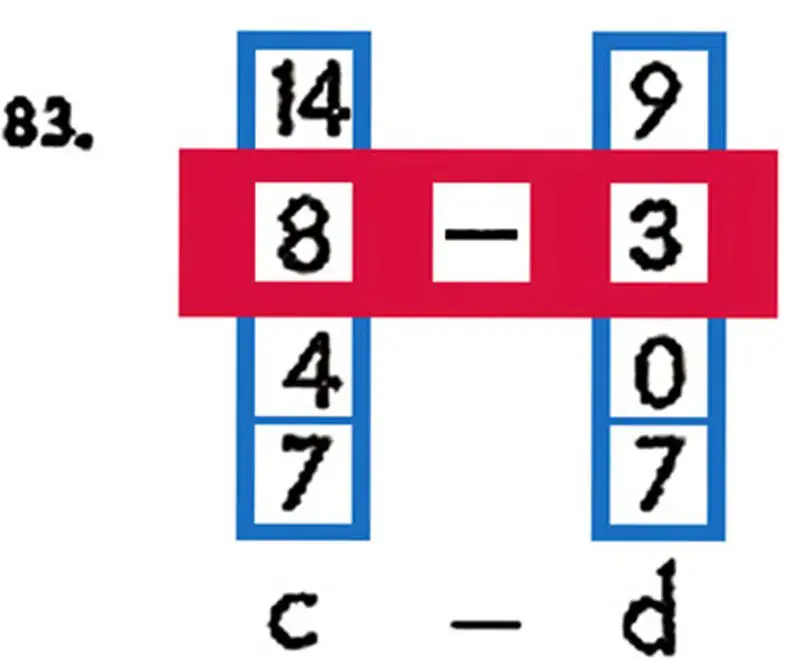
What does the letter c mean?
What does the letter d mean?
What does the expression c – d mean?
Name the numerical values of the letters c and <1.
Calculate the values of the expression c – d with the given values of the letters.
84. In the village, 45 new houses were built: 8 were three-story, 17 were two-story, and the rest were one-story. How many one-story houses were built?
85. On one street in the village, there are 46 houses, on another 5 more, and on the third, there are as many houses as on the first and second together. How many houses are on the third street?
86. Solve the problems with checking: 71—48 67+29
(14+ 7)+(24+6) 67+9-20 х-17=54
(40+18)-(31+19) 68+9-20 с+17=54
( 8+32)+(23+6) 69+9-20 60-«=54
87. (14+ 7)+(24+6) (40+18)-(31+19) ( 8+32)+(23+6)
88. The girl cut off 6 dm from a ribbon and then another 7 dm. After that, she had 9 dm left. How long was the initial piece of ribbon?
89. Pick numbers and solve the problem:
Petya gave … marks to one friend and … marks to another. After that, he had … marks left. How many marks did Petya have initially?
90. What does the expression b+c mean? Find the numerical values of the sum if:
b=46, c=18 b=39, c=39 6=46, c=18 b=39, c=39 b=6, c=87
91. What does the expression a—b mean? P
Find the values of the difference if:
1) a=39, 4=7 2) a=80, 4=56 3) a=49, 4=49
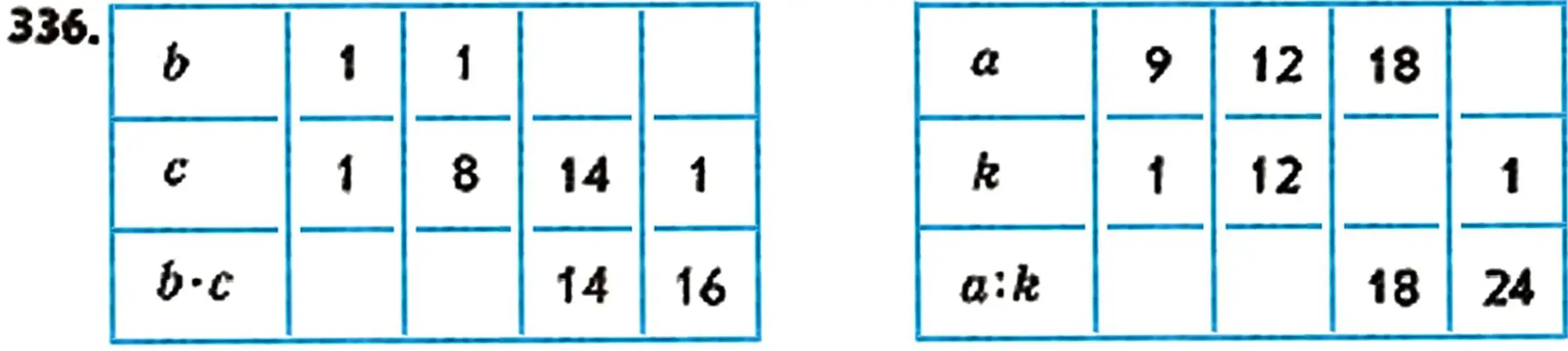
92. Explain each method of solution and calculate the results:
| 58+25=58+(2О+ 5)= | 42-17=42-(10+ 7) = |
| 58+25 = 58+( 2+23)= | 42-17=42-( 2+15) = |
| 58+25=(50+8)+25= | 42-17=(40+2)-17= |
93. 1) How much is 8 less than 30?
2) 16 less than the intended number by 7. What number is intended?
94. Write expressions and calculate their values:
Add the sum of 5 and 15 to the sum of 18 and 12.
Subtract the sum of 31 and 9 from the sum of 7 and 3.
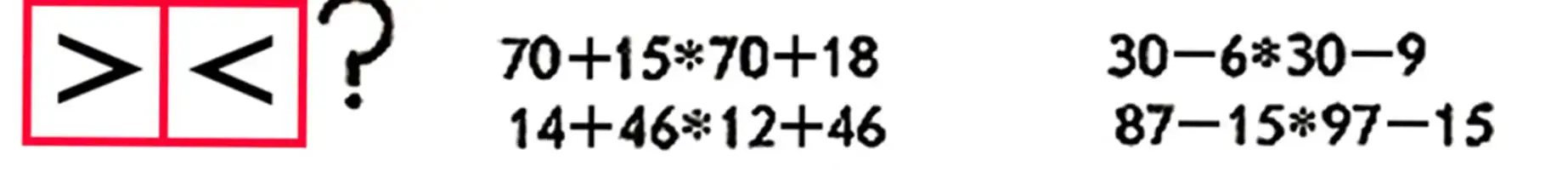
97. Solve the problems. Create reverse problems:
1) A sports jacket and trousers together cost 32 rubles. The jacket costs 22 rubles. How much do the trousers cost?
2) There were 90 cars in the car park. In the morning, 80 cars went on routes. How many cars are left in the park?
| a | 64 | 53 | 42 | 40 | 25 | 16 | 12 | 8 |
| b | 9 | 16 | 28 | 40 | 25 | 30 | 54 | 42 |
| a+b |
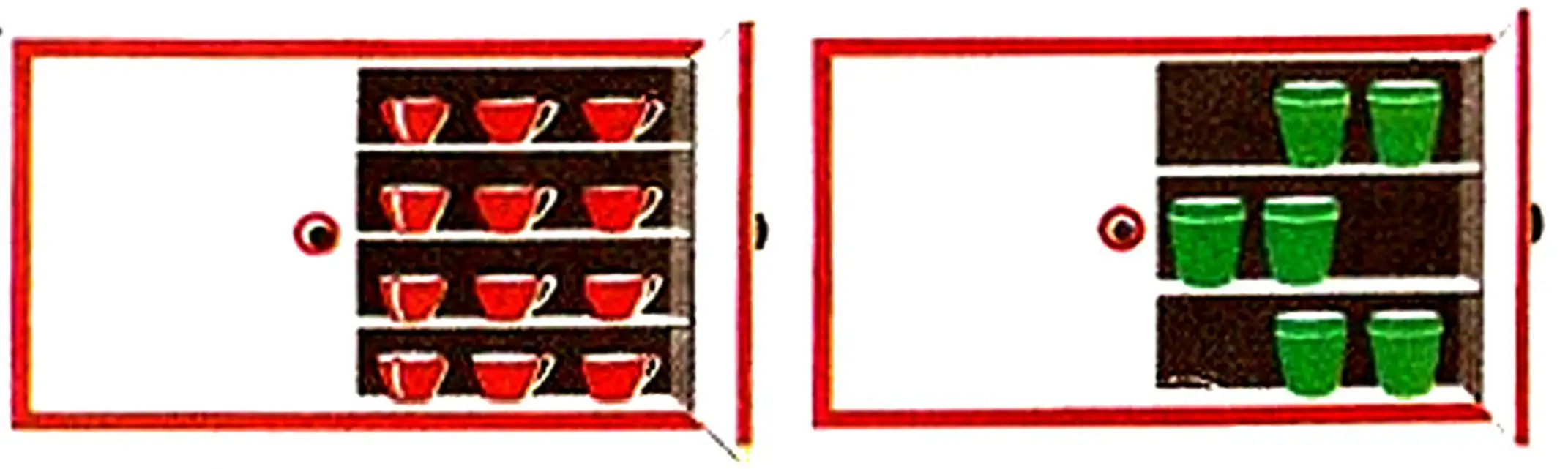
99. Workers from the factory went to a one-day rest house in three buses: the first had 35 people, the third had 5 people less than the first, and the second had 8 people more than the third. How many workers were in the second bus?
100. 42+17-42 (39+16)+(8+22)
16+65-65 (12+46)+(7+13)

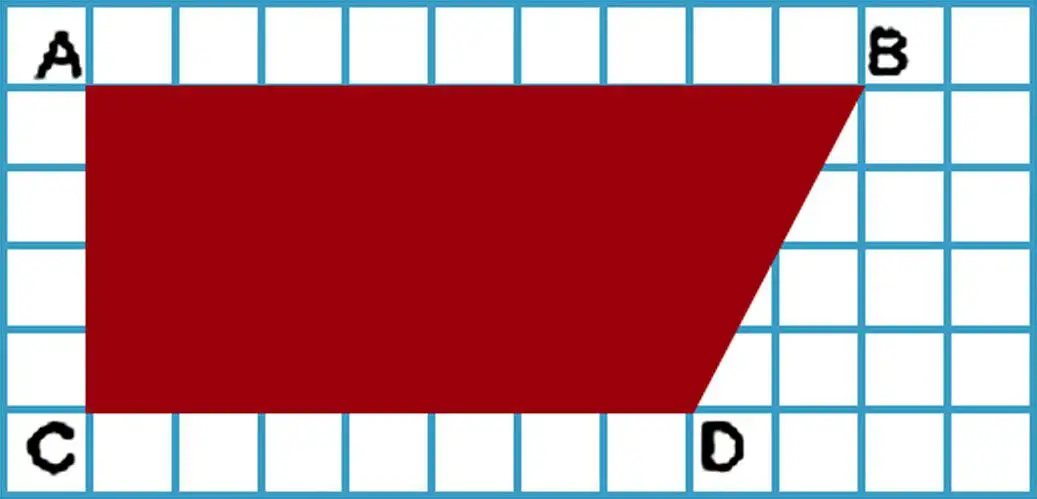
101. Mark the points as shown in the diagram and connect them with segments to form a quadrilateral. What is this quadrilateral called?
Adding the sum to the sum.
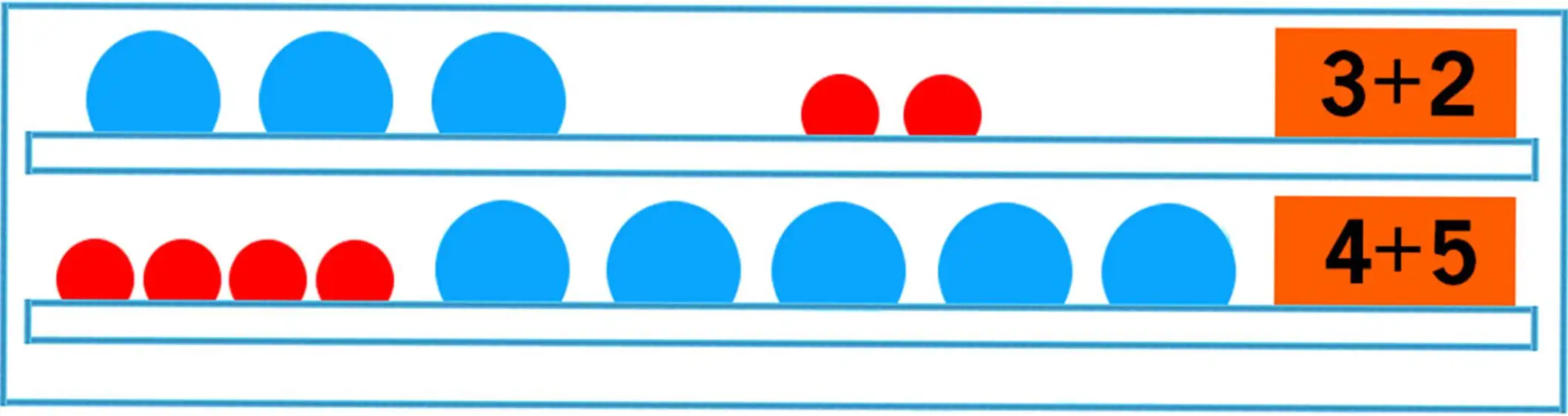
102. 1) (3+2)+(4+5)=5+9=14
You can calculate the sums and add the obtained results.
2) (3+2)+(4+5)=(3+4)+(2+5)=7+7=14
You can add the first addends of these sums, then the second addends, and add the obtained results.
How can you add the sum to the sum?
Solve in different ways: (7+2)+(3+8).
103. Solve in a convenient way: (9+6)+(4+1) (10+5)+(30+4)
(8+2)+(3+4) (20+7)+(40+5)
104. From a jug, they drank 5 glasses of milk, and there were still 3 glasses left. How many glasses of milk were in the jug? Create two reverse problems and solve them.
105. From the classroom library, 35 books were issued. When the teacher issued an additional 8 books, there were 57 books left in the library. How many books are there in the library in total?
107. (30+7)+(10+4) 5+48-35 х-15=70
(16+9)+(21+14) 9+62-27 24-х=8
108. Explain the solution to the examples:
1) 35+21=(30+5)+(20+1)=(30+20)+(5+1)=56
2) 27+16=(20+7)+(10+6)=(20+10)+(7+6)=43
When adding two-digit numbers, you can add the tens to the tens and the ones to the ones.
109. Solve with explanation: 62+34, 28+35.
110. 37+23 16+16+16 45-15-15 9+0 16+82 18+18+18 51-17-17 0-0 45+48 24+24+24 72-18-18 0+0
111. Create a problem using a concise notation and solve it in different ways:
There were 17 and 10.
6 left. What is left?
112. The postman needs to deliver 18 magazines. In one house, he delivered 6 magazines, and in another, 7 magazines. How many more magazines does he need to deliver to readers?
113. How many times are 3 cars drawn? How many cars are there in total?
Draw 2 flags 3 times. How many flags did you draw in total?
114. Draw 8 circles in rows of 4 circles each. How many rows did you get?
115. Choose such numbers that the statements are true:
8 + 44 < 8 + __ 58 — 6 > 58 — __
30 — 5 > __ — 5 20 — 3 < __ — 3
116. Any point on the drawing can be given a “name” by placing a Latin letter next to it. Read the names (designations) of the points on the drawing.
117. Mark three points in your notebook and label them with letters.
118. Draw a segment of length 4 cm. Label the points by letters. It can be said that the segment LV is 4 cm long.
A segment can be denoted by any two letters.
119. Read the names of the segments on the drawing. Compare the segments using a compass. Write like this: AB=CD, AB>KE.
120. Draw three segments, label them with letters, and compare them.
121. Create problems based on expressions: 1) 16+14 2) 50—(16+14)
122. There were 90 liters of kerosene in a barrel, and 56 liters were sold. How many liters of kerosene are left in the barrel? Create two reverse problems and solve them.
123. The tractor driver used 48 liters of fuel, which is 32 liters less than he had left. How many liters of fuel are left?
124. a—e. Choose values for the minuend and subtrahend. Calculate the values of the difference.
125. 28+36 12+12+12+12 42-(12+9)
77+14 13+13+13+13 (50+8)—20
16+45 14+14+14+14 (65+17)-7
126. Explain different methods of subtracting one sum from another.
1) (7+5)—(3+4)=12-7=5
2) (7+5)—(3+4)=(7—3)+(5—4)=4+1=5
3) (7+5)—(3+4)=(7—4)+(5—3)=3+2=5
Compare the results. How can you subtract one sum from another?
127. Solve in different ways: (10+6)—(3+2).
128. Solve using a convenient method:
(20+5)-(10+2) (26+4)-(7+3)
(60+7)-(40+5) (56+35)-(26+15)
129. 1) In January, Borya read 10 books, and in February, 8 books. How many books did Borya read in these two months?
2) In January, Kolya read 6 books, and in February, 4 books. How many books did Kolya read in these two months?
3) In January, a student read a books, and in February, 6 books. How many books did the student read in these two months?
130. There were 80 tomatoes in the basket. For lunch, they ate
10 tomatoes, and for dinner, 16 tomatoes. How many tomatoes are left in the basket? Solve the problem in different ways.
131. Draw two segments. Segment AC=6 cm, segment B K is 2 cm longer.
132. 96-45 73-25 & (60+8)—(10+3) 25+25
94-45 73-27 (70+5)-(60+2) 26+26
133. Solve the examples using a convenient method: (70+8)-(30+6) (50+9)-(20+7)
134. Explain the solution to the example:
37-14=(30+7)-( 10+4)= =(30-10)+(7-4)=23
135. Solve with explanation: 65—21, 87—53.
136. 76-34 18+45 9+16-7 76+24-83 89-51 28-26 8+39-5 17+38-44
137. Sergey bought a coat, shoes, and a hat. The total cost of the purchase was 48 rubles. The coat costs 37 rubles, and the shoes 6 rubles. How much does the hat cost?
138. In the furniture store, they brought 15 wardrobes, 25 beds, and tables were 8 less than the sum of wardrobes and beds combined. How many tables were brought?
139. Increase each of the following numbers by 7: 6, 8, 9, 14, 15, 17, 39, 58.
140. Write down numbers that are greater than 65 and less than 75. Reduce each of them by 47.
141. If you distribute 6 sticks equally between two girls, how many sticks will each girl get? Draw a picture for the problem and solve it.




142. How many groups of three horses are there in the picture? How many horses in total?
Additional exercises.
1. 1) 10+7 30+50+20 45-5+30 80-1-9
16-6 80-30-10 87-80+20 59+1-60
8+70 50+40-60 36-6+70 60-1-50
95-90 30+70-80 27-20+60 79+1+7
|
2) 26+3 |
70-5 |
86-4 |
66-40+4 |
27-27 |
|
26-3 |
46+4 |
70-3 |
80-7+20 |
35+0 |
|
47+30 |
20-7 |
39-20 |
58-6+8 |
54-0 |
|
3) 9+7 |
16-7 |
16+7 |
43-7 |
39+4-7 |
|
5+8 |
12-8 |
27+8 |
24-6 |
55+8-5 |
|
6+6 |
17-9 |
49+6 |
31-8 |
46+7-9 |
|
9+9 |
15-8 |
87+4 |
73-5 |
53+9-6 |
|
4) 50+14 |
27+34 |
21-16 |
29+53 |
31-22 |
|
50-14 |
35+28 |
35-18 |
94-76 |
64+28 |
|
25+12 |
56+17 |
42-24 |
16+37 |
73-37 |
|
25-12 |
18+44 |
56-19 |
83-45 |
52+19 |
|
5) 38+39 |
62-24+37 |
60-23+18 |
44+17-30 |
|
51-17 |
18+35-26 |
87-54+29 |
55+17-30 |
|
27+27 |
80-56+37 |
50-16+37 |
66+17-30 |
|
6) 6-6 |
6+0 |
0+6 |
6-0 |
25+0 |
|
17-17 |
17+0 |
0+17 |
17-0 |
36-36 |
|
24-24 |
24+0 |
0+24 |
24-0 |
0+7 |
2. Write down the numbers that are greater than 25 and less than 31.
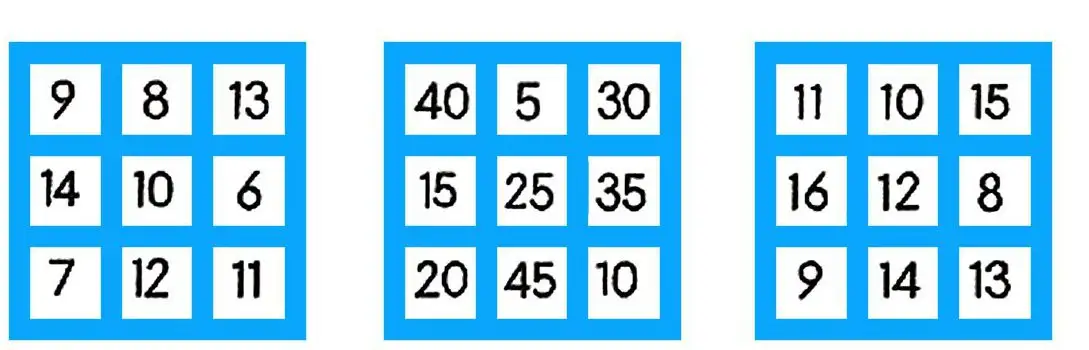
3. Check if the squares are magic:
4. Mazes (game).
5. Write down all possible addition examples of one-digit numbers with the answer 12 (13, 14, 15).
6. Create and solve 4 subtraction examples of two-digit numbers with the answer 5.
|
19+17 |
22+28 |
90-26 |
100-24 |
|
19+15 |
24+28 |
92—26 |
100-22 |
|
19+18 |
26+28 |
94-26 |
100-20 |
|
19+14 |
28+28 |
96-26 |
100-18 |
8. Write down all one-digit numbers. Increase each of them by 8, 9, 24, 37.
9. Insert operation signs instead of asterisks to make the equations true:
|
28*15=13 |
75*7=82 |
12+9*35=56 |
|
36*18=54 |
90*6=84 |
49+8*18=39 |
|
94*0=94 |
14*14=0 |
83-6*12=89 |
11. Fill in the missing numbers in the entertaining frames.
12. Find numbers to make the equations true:
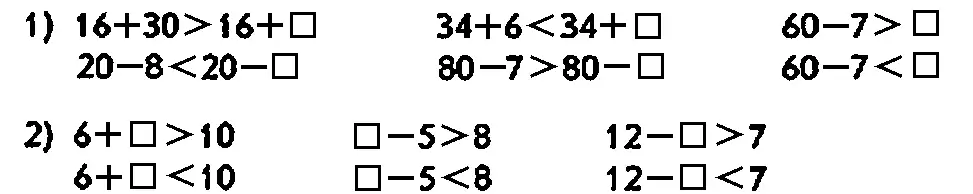
13. 1) Write down the sum of numbers c and 4. Calculate the sum if c=32, d=7; c=14, d=30; c=40, d=40; c=99, d=1.
2) Write down the difference between numbers a and 6. Choose 4 values for each of the subtrahends and calculate the difference.
14. 1) Write down the sum of numbers 6 and 4. Choose 4 values for each of the addends and calculate the sum.
2) Write down the difference between numbers a and 6. Choose 4 values for each of the minuends and subtrahends and calculate the difference.
15. 1) How much is 40 greater than 7?
2) An unknown number is greater than 40 by 7. Find the unknown number.
16. 1) How much is 9 less than 45?
2) 18 is less than an unknown number by 6. Find the unknown number.
17. 1) Schoolchildren planted 24 pear trees, and there are 9 more apple trees than pear trees. How many apple trees did the schoolchildren plant?
2) A gardener pruned 16 poplar trees, which is 5 more than linden trees. How many linden trees did the gardener prune?
18. 1) The factory workers had cars, and motorcycles were owned by 55 more people. How many workers had motorcycles?
2) The factory had 10 buses and 48 trucks. How many more trucks were there in the factory than buses?
19. 1) In a new building, there are 80 apartments, 16 more than in the old one. How many apartments are there in the old building?
2) In the old building, there are 30 apartments, 15 fewer than in the new one. How many apartments are there in the new building?
20 1) Vitya’s mom is 32 years old. She is 8 years younger than Vitya’s dad. How old is Vitya’s dad?
2) Vitya’s sister is 8 years old. She is 6 years older than Vitya. How old is Vitya?
Who is the youngest in Vitya’s family?
21. Compare the segments using a compass that are the sides of each of the drawn triangles.

22. How many triangles and quadrilaterals are in each of these figures?


23. At a gas station, three cars were given 95 liters of gasoline. One was given 40 liters, the second 25 liters. How many liters of gasoline were given to the third car?
24. A teacher gave out 35 grid notebooks and the same number of lined notebooks to children, after which she had 18 notebooks left. How many notebooks did the teacher have?
25. For roof repair, 35 sheets of iron were brought on one car, 37 sheets on another, after which 18 more sheets were needed. How many sheets of iron in total were used for roof repair?
26. Solve problems by composing equations.
1) Subtract 7 from which number to get 27?
2) What number should be added to 43 to get 52?
3) Which number should be subtracted from 40 to get 13?
4) Misha found 12 white mushrooms, and Nina found several white mushrooms. In total, they found 20 white mushrooms. How many white mushrooms did Nina find?
5) For the school repair, several boxes of nails were brought. When 8 boxes of nails were used up, 4 boxes remained. How many boxes of nails were brought for the school repair?
6) There were 27 airplanes at the aerodrome, some of them flew away, after which there were 15 airplanes left at the aerodrome. How many airplanes flew away?
27. Create equations and solve them:
1) x + =12 2) a-7=30 3) 47-b=34
28. There are 20 classrooms in the school, and there are 8 fewer offices. How many total educational rooms are there in the school?
29. Pioneers planted 16 maple trees near the school, and there are 4 more oak trees than maples. Pose a question in a way that requires two operations to solve. Solve the problem.
30. Two swimmers swam towards each other in the lanes of the pool. One swam 27 m to the meeting point, and the other 4 m less. What is the length of the track?
31. 1) Draw two segments: the length of the first is 7 cm, and the second is 5 cm longer. What is the length of the second segment?
2) Draw two segments: the length of the first is 11 cm, and it is 4 cm longer than the second. What is the length of the second segment?
3) Draw two segments: one is 12 cm long, and the other is 9 cm. How many centimeters longer is the first segment than the second one?
32. Draw on graph paper and cut out two quadrilaterals and two triangles as shown in the picture. Compose: 1) a triangle, 2) different quadrilaterals, 3) a hexagon.

33. In a sewing workshop, there were 38 spools of black thread and 35 spools of white. 18 spools of thread were used in one day. How many spools of thread are left?
34. For the holiday, second graders made 52 red flags and 36 blue ones. They gave 25 flags to first graders. How many flags do they have left?
Translation:
[35. On one car, they took away 28 sacks of grain, on another 6 sacks more than on the first, and on the third, 4 sacks less than on the second. How many sacks of grain were taken on the third car?
36. In the garden, there were 18 black currant bushes, white ones were 6 bushes less than black ones, and red ones were 5 bushes more than white ones. How many bushes of red currants were in the garden?
37. In the village, there are 15 four-story houses, 29 two-story houses, and one-story houses are 38 more than four-story and two-story houses together. How many one-story houses are in the village?
38. The young pioneers collected 26 baskets of cherries, 32 baskets of cherries, and plums were 5 baskets more than cherries and cherries together. How many baskets of plums did the young pioneers collect?
39. From the first apple tree, they collected 38 kg of apples, from the second 2 kg more than from the first, and from the third 8 kg less than from the first. How many kilograms of apples were collected from the second apple tree, and how many from the third one?
40. The teacher wrote 20 examples on the board. By the end of the lesson, Sasha managed to solve 12 examples, and Lena 18. Who of them has more examples left to solve, and how many?
41. A bridge was built across the river with a length of 56 meters. Add to the problem so that you can find out the width of the river.
Multiplication and Division. Multiplication.


143. 2+2+2+2+2=10
2 x 5=10
Adding identical summands is called multiplication. The sum of identical summands 2+2+2+2+2 can be written as: 2 x 5.
The dot (•) is the multiplication sign.
Examples of multiplication are read as follows:
2*5=10 take two five times, it will be ten or two multiplied by five, it will be ten.
Read the following examples and solve them:
7+7+7=21 3+3 =
7*3=21 3-2 =

144. Find the values of the expressions c + d and c – d, if c=16, d=14; c=33, d=15; c=48, d=48.
145. Draw two segments: AB=9 cm, CD=7 cm. How many centimeters is segment CD smaller than segment AB?
146. The Pioneer squad was given a task to fix 80 books. The first link fixed 16 books, the second 18 books. How many books are left to fix?
147. Children took 46 books from the class library, which is 39 books less than remained. How many books are left in the library?
14 8.1) Decrease each of the numbers by 28: 60, 31, 54, 83.
2) Increase each of the numbers by 39: 8, 17, 43, 26.
149. Replace the examples with multiplication examples:
3+3+3+3+3= 6+6+6+6+6=
150. Calculate the results and replace, where possible, examples with addition examples with multiplication:
$+8+8+8 5+5+5+5+5+5 7+7+7+7
28+82 7+4+47 6+6+6
12+12+12 36+36 4+8+5+9
151. 9+17 16+28 47+36 a+b
17+9 28+16 36+47 6+a
152. The children returned from the pioneer camp in two buses: one had 38 children, the same number in the other; in
total, 43 boys were returning. How many girls were returning from the pioneer camp?
153. In 8 competitions in jumping, 16 girls participated, which is 9 less than boys. How many boys participated in the competitions?
154. (40+7)-(10+5) 8+26-11 M=15
(60+9)-(40+2) 7+35-22 43-a=18
155. 8 x 3
8+8+8=24 What number is taken as a summand?
8-3=24 How many times is the number 8 taken as a summand?
156. Replace the examples with multiplication examples and calculate the results: 5×3 3*2 4*4 10-5 2*7
157. Draw the conditions of the problem and solve it:
1) There are 5 apples on each plate. How many apples are on three plates?
2) There are 10 eggs in each box. How many eggs are in two boxes?
158. 1 dm 8 cm = ___ cm 25 dm = ___ m ___ m
4m 2 dm = ____ dm 38 cm = ___ dm ___ cm
|
159. 65-(15+10) |
75+25-14 |
56-56+95 |
87-0 |
|
(67+8)+13 |
90-34+18 |
78+9-87 |
0+38 |
|
(48+21 )-18 |
43+19-34 |
47-8-39 |
16-16 |
Translation:
[160. On the school stadium, the pioneers cleared 45 meters of the running track on the first day, 6 meters less on the second day than on the first, and 8 meters more on the third day than on the second. How many meters of the track were cleared on the third day?
161. Draw a rectangle with sides of 6 cm and 8 cm. Draw one segment in it so that two triangles are formed. Measure the sides of one triangle.
Division.

162. 8 oranges were divided onto plates, 2 oranges per plate. How many times were 2 oranges placed? How many plates were needed?
This problem was solved by division. Two dots (:) are the division sign.
The solution to the problem can be written as follows:
8:2=4 Answer: 4 plates.
163. Grandma had 10 carrots. She tied them in bundles of 5 carrots each. How many bundles did she get?
10:5=2 Answer: 2 bundles.

164. Find the result using the diagram:

9 : 3 = 12 : 3 =
165. Write down multiplication examples and calculate the result, replacing them with addition examples:
1) take 9 four times 3) take 10 three times
2) take 4 six times 4) take 15 two times
166. From a spool of wire, they first cut off 18 meters, and later another 9 meters. After that, 7 meters of wire remained on the spool. How many meters of wire were there initially?
167. Compose a problem based on the concise expression and solve it:
168. 96-06+30) 79-25+38 7+86-52
96-46+30 51-17-17 8+35-42
There were 32, 8 left, and 15 left. How many are left?
169. Illustrate the conditions of the problems and solve them:
1) 6 pieces of sugar were distributed on tea saucers, 2 pieces per saucer. How many saucers were enough for this sugar? 2) 12 radishes were tied into bundles, 6 radishes per bundle. How many bundles were formed?

170. There were 4 jars of fruit juice on the table, each containing 3 liters. How many liters of juice were in these jars?
171.
172. (a+9)+c.
Evaluate the value of this expression if a=24, c=32; a=77, c=13.
173. In the collective farm, 24 people worked on the poultry farm, and on the dairy farm, there were 56 people; in total, 38 men worked on these farms. How many women worked on these farms?
174. (45+17)+(5+23) 54-(17-9) 41-(24+8)
(78+16)-(8+15) 54-17-9 41-24+8
176. The first factor is 2, the second is 4. Find the product. What does the first factor show? The second factor?
177. Write down and calculate the product of the numbers 5 and 2, 7 and 3, 2 and 6.
178. A pencil costs 4 kopecks. How many kopecks do you need to pay for 2 such pencils? for 4 pencils? for 5 pencils?
179. The teacher distributed 12 notebooks to the students, 2 notebooks per student. How many students received notebooks?
180. In the singing club, 42 students were engaged, in the drawing club, there were 5 students less than in the singing club, and in the sports club, there were as many students as in the singing and drawing clubs together. How many students were in the sports club?
181. 49+18
-49 x+17=40 7m4dm <^ = _dm
56-47+18 a-16=40 5dm7cm = __ cm«
96—26—64 31—2=9 49 cm=_dmamp;»<__cm
182. Draw such a quadrilateral and draw one segment in it so that: a) a rectangle and a triangle are formed; b) a square and another quadrilateral are formed.
Millimeter.

183. Point to the centimeter on the ruler. Count how many equal parts a centimeter is divided into. Each such part is a millimeter.
10 divisions = 1 cm
184. Measure the segments and write down the lengths of each of them.
Sample recording: OK = 1 cm 2 mm
185. Draw segments with lengths of 8 mm, 5 mm, 7 mm
2 cm 3 mm, 4 cm 2 mm, 1 cm 6 mm.
186. Name the factors in the following products:
3-5, 4-4, 9-2, 8-3, 1-6. Replace the products with sums and calculate their values.
187. 3 boxes of oranges were delivered to the cafeteria, 9 kg in each. How many kilograms of oranges were delivered?

188. Mom gave out 12 apples to the children, 4 apples per child. How many children received apples?
189. Compose a problem based on the expression: (17+15)—14.
Solve the problem in different ways.
Here’s the English translation:
[190. 89 – (56 + 13) 32 + (7 + 28) 19 + 19 + 19 + 19
68 – (25 + 18) 56 + (19 + 21) 81 – 27 – 27 – 27

191. 12 pencils were distributed evenly among 3 students. How many pencils did each student receive? 12 – 3 = 4 Answer: 4 pencils.
192. Take 6 cups from the set and divide them into 2 equal parts. How many cups are in each part?
193. The teacher distributed 10 notebooks equally among 5 students. How many notebooks did each student receive?
194. Measure the length of each side of the following figures:
Sample recording: AB = 1 cm 7 mm.
195. 1 cm 3 lig = □ lig 16 lig = □ cm □ lig
5 cm 8 mm = □ mm 74 mm = □ cm □ mm
196. Calculate the results and replace the sums with products:
E + 8 + 8 + 8 1 + 1 + 1 + 1 + 1 14 + 14 + 14
State the factors, state the products.
197. The height of each floor is 4 m. The building has 5 floors. What is the height of the building to the roof?
198. In three days, workers repaired 24 trolleybuses: on the first day — 8 trolleybuses, on the second — 10. How many trolleybuses did they repair on the third day?
|
a |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
|
c a-c |
7 |
12 |
19 |
26 |
34 |
41 |
48 |
Does the minuend change? How does the subtrahend change? How does the difference change?
200. Sketch the problem and solve it.
1) 8 carrots were distributed evenly among 4 rabbits. How many carrots did each rabbit receive?
2) 15 carrots were given to rabbits, 5 carrots each. How many rabbits received carrots?



201. Create problems based on the drawings and solve them.
202. From the series of numbers 7, 8, 9, 10, 11, 12, 13, 14, extract the values of the variable “a” for which the inequality a-7<5 is true.
203. Write down the products of the numbers 8 and 4, 10 and 3, 12 and 2. Calculate the products, replacing them with sums.
204. Lesha bought 4 floats, each costing 3 kopecks. How much did all the floats cost?
205. Create problems based on the expressions and solve them: 1) 17 + 19 2) (17 + 19) – 8
206. (45 + 37) – (27 + 10)
207. To decorate the Christmas tree, boys cut out 28 red flags and 10 green ones, while girls cut out 40 blue flags. How many more flags did the girls cut out?
208. For the holiday
decoration, 12 girls and 9 boys decorated the class. Then 5 girls went home. How many more boys remained than girls?
209. Examine the picture and create a multiplication problem based on it.
210. Each coat needs to have 4 buttons sewn on. How many buttons do you need to sew on 6 such coats?
211. Draw a rectangle with sides 5 units and 5 units: and 3 units and 5 tenths.4/4.
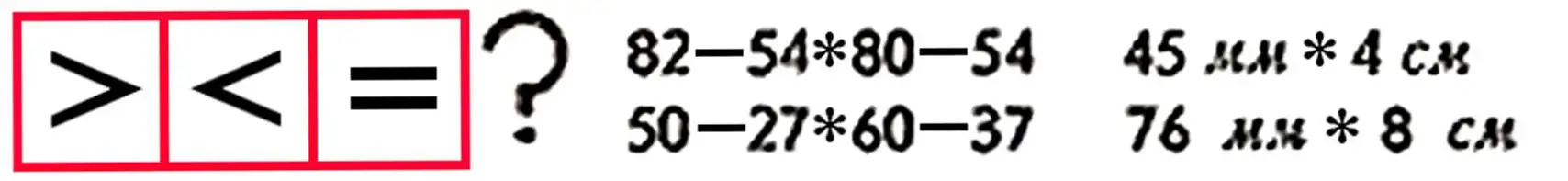
213. 54-20-12 36-8-9 84-8+8+8+8
e 54-(20-12) 36-(8+9) 9+9+9+9+9
214. Write down the sums for: a=9, 6=4; a=9, 6=7; a=9, 6=9; a=9, 6=15.
The first addend does not change, it is 9. The second addend changes, it takes various values. The sum can be written as: 9+6. 215. 1) c-d. Choose values for c and d so that the minuend changes, and the subtrahend does not change. How can you then write the difference?
2) 40-k. Calculate the values of the difference if k takes values: 40, 37, 31, 18, 0.
What changed? What did not change?
216. 1) The first factor is 10, the second is 3. Find the product.
2) Write down the products of the numbers 8 and 5, 9 and 2, 4 and 6. Replace the products with sums and find their values.
217. In the collective farm garage, there were 24 trucks and 9 cars, then 17 trucks left for work. How many fewer trucks remained than cars?
218. 1) For pickling, 5 jars were filled with 8 cucumbers each. How many cucumbers were there in these jars?
2 ) Young pioneers planted birches in 2 rows, with 10 birches in each. How many birches did the Young Pioneers plant in total?
219. Insert the + or — sign and the missing number to make the statements true:
56 * 0 = 38 47 * 0 = 47 76 * 0 = 80 90 * 0 = 15
Commutative property of multiplication.
220.1) Examine the picture:
>6-4 63=3 6
2) 5 * 2=10 5*2 2*5

The product does not change when the factors are rearranged.
221. Copy, filling in the missing number:
7-4=4-__ 9 ___ =7-9 13-5 = ___ 13
3 5=__3 ___ 6 = 6 – 10 __ 18 = 18 – 2
222. 1) Dad bought 2 bags of potatoes, each weighing 3 kg. How many kilograms of potatoes did Dad buy?
2) Mom bought 3 bags of flour, each weighing 2 kg. How many kilograms of flour did Mom buy?
223. 39 + a. Calculate the values of the sum if a takes values: 0, 6, 15, 31, 46, 52.
224. b-18=46 x+27=80 62-x=15
225. Nadia had a 50 kopeck coin. She bought a pen for 35 kopecks and a notebook for 2 kopecks. How much change did Nadia receive?
Below is the translation of the provided text into English:
“`plaintext
226.
|
a |
b |
a-b |
b-a |
|
6 |
2 |
||
|
8 |
4 |
||
|
10 |
3 |
ab=ba
|
5-8=40 |
7-9=63 |
9-8=72 |
12-5=60 |
|
8-5= |
9-7= |
8-9= |
5-12= |
228. 1) How much do 6 pillows weigh if each weighs 2 kg?
2) How much do 2 sheets of iron weigh if each weighs 6 kg?
229. 8 boys gathered to play football; they split into two equal teams. How many boys were in each team?
230. 15 boys divided into squads of 5 each for a game. How many squads were there?
231. Create problems based on the expressions: 1) 24—7 2) 40—(24—7)
232. 74-48+18
74—(48+18)
74-(48-18)
|
74-48+18 |
6+28-31+8 |
7+7+7+7 |
|
74-(48+18) |
9+47-29-27 |
6+6+6+6 |
|
74—(48—18) |
5+59-12+9 |
4+4+4+4 |
233. Draw and cut out one rectangle and four triangles as shown in the picture. Form from these figures: 1) a triangle, 2) different quadrilaterals, 3) a hexagon.

234. Calculate the products by replacing them with sums: 8-2 2-8 3-7 7-3 5-7 7-5
It is more convenient to multiply the larger number by the smaller one.
235. Calculate the products using a convenient method:
5*3 2-7 3-9 4-6 2*10 8-4
236.
|
a |
16 |
16 |
16 |
16 |
|
b |
7 |
9 |
16 |
28 |
|
a+b |
Fill in the table. Name the values of the first addend, the second addend, and the sum. Which addend values do not change?
This table can also be written shorter like this:
|
b |
7 |
9 |
16 |
28 |
|
16 + b |
How do the addends change, how does the sum change?
237.
|
c |
80 |
80 |
80 |
80 |
|
d |
6 |
27 |
49 |
64 |
|
c-d |
Examine the table and fill it in. How can you write this table in a shorter way?
238. There were 20 cars in the garage, with 10 cars in each row. How many rows were there?
239. 12 lifting cranes were sent to two construction sites, divided equally for each. How many cranes were sent to each construction site?
240.  
; Fill in the missing numbers and solve the problem:
Mom gave Vasya 1 ruble and asked him to buy bread for … kopecks and a pack of cookies for … kopecks. How much change will Vasya bring back?
Finding the unknown multiplier.


If the product of two numbers is divided by one of the multipliers, the result is the other multiplier.
243. Calculate the products:
|
7*2= |
8*3 = |
9*2= |
10*3 = |
|
14:7 = |
24:8 = |
18:9= |
30: 10 = |
|
14:2= |
24:3= |
18:2= |
30:3= |
How did you obtain the first multiplier? How did you obtain the second multiplier?
244. For one child’s dress, 2 meters of fabric are used. How many meters of fabric will be needed for 3 such dresses? for 4 dresses? for 6 dresses?
245. Two boxes of carrots were delivered to the store: the first one had 15 kg, and the second one had 21 kg. Yulia bought some carrots from the first box. How many kilograms less carrots are left in the first box than in the second one?

246. How many millimeters is segment AB shorter than segment CD?
247. (73+18)-(8+53) 86-79+54 a-42=38
(20+9)+(40+8) 92-84+17 16-c=9
248. The first multiplier is 4, the second one is unknown, and the product is 8. Find the second multiplier.
249. x 2=6 5 a=10 3-6=9 ^ 3=6
250. From the series of numbers 18, 19, 20, 21, 22, name the values of c for which the expression is true: x—15<5.
|
b |
17 |
24 |
29 |
32 |
40 |
54 |
70 |
81 |
|
c |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
|
b+c |
Write this table with two columns.
252. Pioneers planted 16 currant bushes, 4 bushes in each row. How many rows were there?
253. Children planted 15 oak trees in 3 identical rows. How many oak trees were there in each row?
254. A drawing notebook costs 6 kopecks. How much money do you need to pay for 2 such notebooks? for 3 notebooks? for 5 notebooks?

Translate to English:
“`html
255. Using the drawing, explain what the following expressions represent:
|
1) 8+5 |
2) 8+2 |
3) 5+2 |
4) 8-5 |
|
5) 8-2 |
6) 5-2 |
7) 8+5+2 |
8) 8-(5+2) |
|
256. 5 dm = □ cm |
30-(17+5) |
94-8-16 |
|
5 cm = □ mm |
30-07+6) |
76+24-7 |
|
5 L = □ dm |
30-(17+7) |
32-16-16 |
258. Find the quotient using bars:
1) Dividend 6, divisor 3. Find the quotient.
2) Divisor 2, dividend 8. Find the quotient.
3) Find the quotient of the numbers 12 and 6.
259. 12 knives were packed in boxes, 6 knives in each. How many boxes were needed?
260. From 18 skeins of wool, 6 identical scarves were knitted. How many skeins went into each scarf?
261. How many wheels are needed for 5 bicycles with two wheels each?
262. Find the unknown factor: x*10=20 2*a=8 k*5=10 4*a=8
|
a |
70 |
74 |
80 |
83 |
90 |
92 |
95 |
97 |
|
k |
46 |
46 |
46 |
46 |
46 |
46 |
46 |
46 |
|
a-k |
Organize this table with two columns.
264. Mom milked the cow. She poured 2 liters of milk into a jug and the rest into a can. How many liters of milk did our cow give if mom poured 3 liters more into the can than into the jug?
266.1) For a living corner, 8 rabbits were bought and placed in cages in pairs. How many cages were needed?
2) For a living corner, 8 rabbits were bought and placed in 2 cages equally. How many rabbits were placed in each cage?
267. What division examples can be solved knowing that 7-3=21?
268. 8-5=40 40:8=
3-6=18
18:6=
7-9=63
63:7=
9-4=36
36:9=
269. Skis cost 8 rubles, 6 rubles more than the poles for them. How much do ski poles cost?
270. For the apartment renovation, 10 cans of paint were bought, and 7 cans were used. How many more cans of paint were used than left?
Illustrate the problem and solve it.
271. 65-28-30 29+17+11 (76+8)-76
74-35-18 38+26+12 35-(7+8)
272. 1) Divide a segment of length 12 cm into 2 equal parts. What is the length of each part?
2) Divide a segment of length 12 cm into parts, each 2 cm. How many such parts are there?
273. A doll costs 5 rubles. How much do 3 dolls cost?

274. Compose two problems on finding the cost, write them briefly in the table, and solve them.
275. a-7=14 a+9=12 a-8=17 10*x=20
276. Solve the second example of each pair using the first one:
9-7=63 7-10=70 15-4=60 14-5=70
9-8= 7-9= 15-5= 14-4 =
277. The ruler, pencil case, and album cost 95 kopecks. The ruler costs 12 kopecks, and the pencil case is 48 kopecks. How much does the album cost?
278. Examine the figures on the drawing. How to draw one line in each of these figures so that a square is obtained?
279. (25+29)-26 78-(50+8) 60-15+9
(35+18)-42 37-(7+3) 32-17+8
(42+54)-34 82-(12+30) 73-28+9
280. Vanya collected a collection of butterflies in the summer: in three boxes, he had 6 butterflies each, and in one box, there were 4 butterflies. How many butterflies did Vanya have in total?
281. On one bed, tomato bushes were planted in 3 rows, with 8 bushes in each, and on another bed, there were 15 bushes. How many bushes of tomatoes were planted in total on these two beds?
282. How much do 3 meters of fabric cost at a price of 4 rubles per meter?
283.1) The Young Pioneers planted 15 linden trees in 3 rows evenly. How many linden trees are there in each row?
2) The Young Pioneers planted 15 linden trees, with 3 trees in a row. How many rows did they get?
284. 6*8=48 4*6=24 9*5=45 10*7=70
7*8= 5*6= 8*5= 9*7=
285
|
c |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
|
d |
2 |
6 |
9 |
14 |
17 |
19 |
23 |
|
c – d |
Organize this table with two columns.
286. 83-40+16 100-45-25 (51+23)-23
92-56+17 100-46-26 (51+23)-24
55-27+38 100-46-27 (18+17)-25
Finding the Unknown Dividend and Divisor
12:4=3
3-4 = 12
6:2=3
2-3=6
If the dividend is divided by the quotient, the divisor is obtained. If the divisor is multiplied by the quotient, the dividend is obtained.
Solve and explain how the second and third examples are derived from the first.
|
18:2= |
10:5= |
8:4= |
15:3= |
|
18:9= |
10:2= |
8:2= |
15=5= |
|
2-9= |
5-2= |
4-2= |
3-5= |
289. On the first day, 28 logs were brought for the school renovation, and on the second day, 4 trucks brought 10 logs each. How many logs were brought in total over these two days?
290. For 10 kopecks, 2 identical candies were bought. How much does one candy cost? Write the problem briefly in the table and solve it.
Here is the translation of the text:
“`html
291. Create two problems on finding the price and solve them.
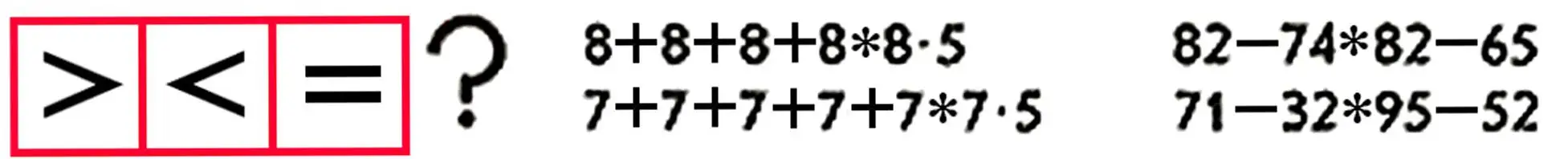
|
1+5+9+15 |
26+19+24 |
89-14-35 |
|
18+7+13+22 |
47+35+13 |
93-48-45 |
294. Check if the =, >, < signs are placed correctly:
9-3=27
6-4=46 17-5=8+4
These are equations.
2-7>2-6
78-9<78 37+6>37
These are inequalities.
295. Write two equations and two inequalities using the expressions:
23+12 40-16 12+23 40-5
296. 8:а=2 с:2=6 b:4=2 12:х=6
297. There were 16 clover leaves in the field. They took away 12 leaves. How many leaves are left, less than what was taken away?
298. How many wheels do four “Volga” cars have?
299. Grandma knitted 4 pairs of mittens for her grandchildren. How many mittens did she knit?
300.
How is the second table derived from the first one?
301.10-3
303 ZOIO
71-68+39 84-35+16
27+9-24
16 mm = □ cm □ mm
27 mm = □ cm □ mm
54 mm = □ cm □ mm
302. 12’4. Let’s choose a number such that when multiplied by the divisor, the dividend is obtained. This number will be 3, because 3*4=12, which means, 12:4=3.
303. 8:4= 6:3= 9:3= 10:5=
4-2=8 3*2=6 3*3=9 5*2=10
304. Farmers went to the city theater. In three cars, 5 people each went, and 35 people went by bus. How many people visited the theater in total?
305. Create a problem similar to problem 304 using the expression: 6*2+9.
306. Tram ticket costs 3 kopecks. The student rode the tram 4 times. How many kopecks did he pay for the tickets?
307. In the first grade, there are д girls and м boys. How many children are there in this class in total?
Solve the problem if а=18, м=20. Choose other numbers and solve the problem.
308. Draw two segments: AB=5 cm 8 mm, and segment CD is 5 cm shorter.
309. Fill in the asterisks with + or — to make the equations correct:
76*20*42=54 89 *23*61 = 5 75*25*30 =70
38 *25* 12 =75 98*75*37= 60 68 *24*56=100
310. Find the result using addition: 1*2 1*3 1*4 1-6 1*а=a
311. 1*14 1*52+18 (80-79)24 1(67+18)
1*38 1*64-36 (60-59)*75 1 (60-27)
1*а 1-42-9 1*(42-24) 1* (55+9)

312. There are 5 riders on 5 horses. How many riders in total?
313. 54*6= 72:8= 35:7= 42:6=
6*9=54 9*8=72 7*5=35 7*6=42
314. 1) Dividend is 12, quotient is 4. Find the divisor.
2) Divisor is 2, quotient is 5. Find the dividend.
3) First factor is 5, product is 10. Find the second factor.
315. 3a 2 packs of salt cost 14 kopecks. What is the price of one pack of salt?
316. In the first dining room, 35 people had lunch, and in the second, 42 people. 11 people left the second dining room. How many more people are there in the first dining room than in the second?
317. 1) Fill in the table:

2) Using the table, indicate those values of the letter b for which the inequality 17+b&<25 is true.
Multiplication by one.
When any number is multiplied by one, the result is the same as the number being multiplied.
For example: 3*-1 =3 42*1=42 89*1=89 a-1=a
319. 7*1 32 (48*47) (70-69)*14 1*83-1
89*1 (61-24)*1 27*(30-29) 27*1-1
320. 36:4=9 42:6=7 28:7=4 40:8=5
9-4= 6-7= 7-4=8-5=
36:9= 42:7= 28:4= 40:5 =
321. Fill in the blanks to make the equations or inequalities correct:
9*6=6 □ 8*2>8*__П 56-24>56-__
7*4=4*__ 9*1 < 9* __ 78+19<78+__
322. 1) A pie costs 5 kopecks. How many pies can you buy for 15 kopecks?
2) Create two problems on finding the quantity from known price and cost. Solve these problems.
323. In three pieces, there are 92 liters of string. The first piece has 28 liters, the third has 34 liters. How many meters of string are in the second piece?
324. Draw such pentagons. In the first one, draw one segment to form a triangle and a quadrilateral, and in the second one, draw two quadrilaterals.
Division by One.
325. Find the result of each first example using the second example:
3:1= 5:1= 1:8 = k: 4=
1*3=3 1*5=5 1*18=18 1*a=a
When dividing any number by one, the quotient is the same as the number.
|
326. 8:1 |
76:1-18 |
(90-45)*1 |
71-45+0 |
|
15 : 1 |
39:1+38 |
1*(36-19) |
65+26-0 |
|
93 : 1 |
52:1-27 |
(24-15): 1 |
14+27+0 |
|
327. b*a=12 |
a:4=8 |
16 = b*16 |
k : 2=6 |
328.
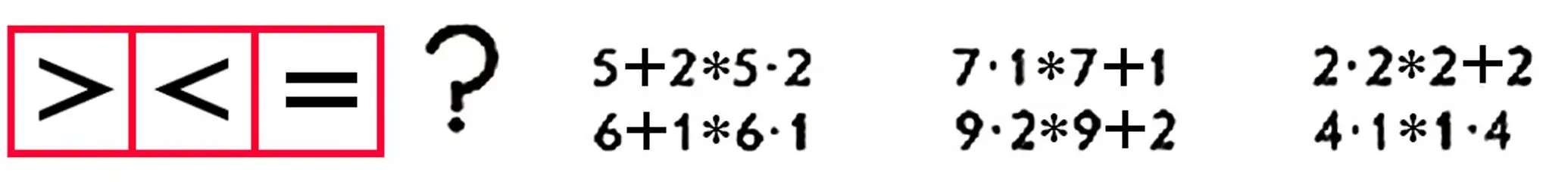
330. For 10 kopecks, envelopes were bought, at 5 kopecks each. How many envelopes were bought? Create two inverse problems and solve them.
331. For winter, the family preserved 8 three-liter jars and one ten-liter jar of apple juice. How many liters of juice were preserved in total?
Multiplication by Ten and Division by 10.
332. Complete the examples. Reason as follows: to multiply by 2, you need to multiply 1 dozen by 2, resulting in 2 dozen, or 20. If:
10-2=20, then 2-10=20 and 20:2=10, 20:10=2,
If the first example in each column must end with 10*10.

|
10*7 |
10*9 |
8*10 |
40:4 |
7*1 |
|
7*10 |
90:10 |
80:10 |
60:10 |
7*10 |
|
70:10 |
9*10 |
80:8 |
30:3 |
9:9 |
|
70:7 |
90:9 |
10*8 |
50:10 |
90:9 |
334. One kilogram of cabbage costs 10 kopecks. How much do 2 kg, 3 kg, 5 kg, and 8 kg of cabbage cost?
335. From one cow, the milkmaid milked 15 liters of milk, from another 17 liters, and from the third 18 liters. She poured all the milk into containers, 10 liters in each. How many containers were needed?
98—(36+18) 29+35 73-5923:23
(52+17)—17 61-48 64+8 48*1
80-(45+15) 47+34 90-59 57:1
338. The cafeteria worker arranged 50
sandwiches on 5 plates, evenly
distributed. How many sandwiches are on each plate?
Additional Exercises.
|
1) 35+8 |
73+19 |
9+64 |
49+25 |
19+19 |
|
14+39 |
17+56 |
17+17 |
58+16 |
19+18 |
|
87+8 |
43+36 |
38+9 |
25+67 |
19+17 |
|
2) 32-3 |
90-78 |
51-34 |
58-34 |
42-13 |
|
46-17 |
100-6 |
23-7 |
14-14 |
42-14 |
|
80-21 |
54-43 |
62-53 |
27-25 |
42-15 |
|
53-35 |
87-70 |
71-17 |
40-3 |
42-16 |
|
3) 51-27-14 |
78-14-38 |
54-5+16 |
8-8 |
|
|
76-17-15 |
27-9+13 |
81+17-18 |
5+0 |
|
|
92-46-22 |
46+25-16 |
22-17+35 |
9-0 |
|
|
4) |
59-9-9 |
70-15-25 |
24+17+13 |
18+0 |
|
38+8+9 |
70-16-26 |
24+18+14 |
0+19 |
|
|
45-16-5 |
70-17-27 |
24+19+15 |
34+34 |
|
|
28+17+12 |
70-18-52 |
24+20+16 |
57-0 |
|
|
5) |
27+35-48 |
80-73+84 |
78+12-8 |
46+0 |
|
65-47+34 |
26+62-50 |
31-19+6 |
32-31 |
|
|
86+14-75 |
30-8+62 |
27+15-9 |
10-0 |
|
2. Replace the examples with addition examples with multiplication:
|
5+5+5 |
6+6+6+6+6 |
7+7 |
|
9+9+9+9 |
4+4+4+4 |
1+1 |
Translate to English:
“`html
3. Replace the examples with multiplication examples: 9-3 4-5 2-4 8-2 9-5
4. Fill in the magic squares:
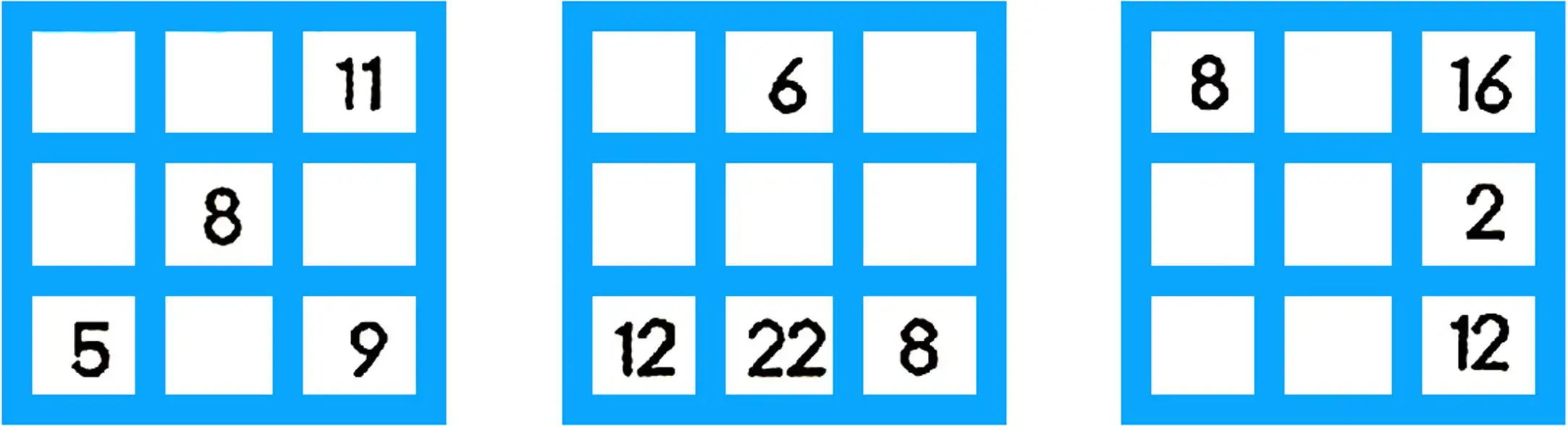
9. Replace the sums with products: 3+3+3 6+6+6+61+1+1
10+10+10+10+10 5+5+5+54+4+4
6. Find the product of numbers 2 and 4, 5 and 3, 1 and 5.

|
8. 1) 7 *1 |
56:56 |
94*1 |
(28-27)-15 |
24:1 |
|
1*8 |
1*42 |
83:83 |
16:(48-47) |
1-24 |
|
2) 5:5 |
35-1 |
1-29 |
91 (78-77) |
24-1 |
|
4:1 |
74:1 |
31:1 |
12:(31-19) |
24:24 |
|
3) 20:10’3 |
5-10-26 |
80:10+49 |
60:10 |
|
40:4-6 |
10-7-38 |
(82-74)10 |
10 6 |
|
100:10-7 |
10-8-25 |
(56+34): 10 |
60:6 |
|
4) (80-79) 36-24 |
8:817+18 |
27:1:27-46 |
|
(68-67)27+35 |
64:64-42-25 |
52=1:52-94 |
|
(20-19) 42-16 |
56:56-74-9 |
38:1:38-15 |
9. 1) 4 cm = □ mm 70 mm = □ cm 30 dm = □ cm
6 cm = □ mm 90 mm: = □ cm 30 cm = □ dm
2) 7 cm > □ mm. 50 mm < □ cm 2 dm < □ cm
2 cm < □ mm 90 mm > □ cm 9 m < □ dm
3) 26+15<26+П 84-(10+5)>84-П
43-17 >43-__ (90+8)-50 > (90+8)-__
10. Solve the equations:
1) b+18=40 94-x=35 75-b=28
b-18=40 26+x=70 b-48=48
80-b=32 x-34=9 56+b=56
11. Mazes.
|
12. 4*7=28 |
5*6=30 |
9*3=27 |
6*4=24 |
|
4*8= |
6 *6= |
9*4= |
7*4= |
|
4*9= |
7*6= |
9*5= |
8*4= |
13. Choose numbers so that the inequalities and equalities are correct.
|
1) 8-3>8-4-__ |
10-6+О10-7 2)3-__=8-3 |
6-4<4- □ |
|
9-5<9-4+П |
3-9-ПО-8 П-9=9-2 |
4*0 >5-4 |
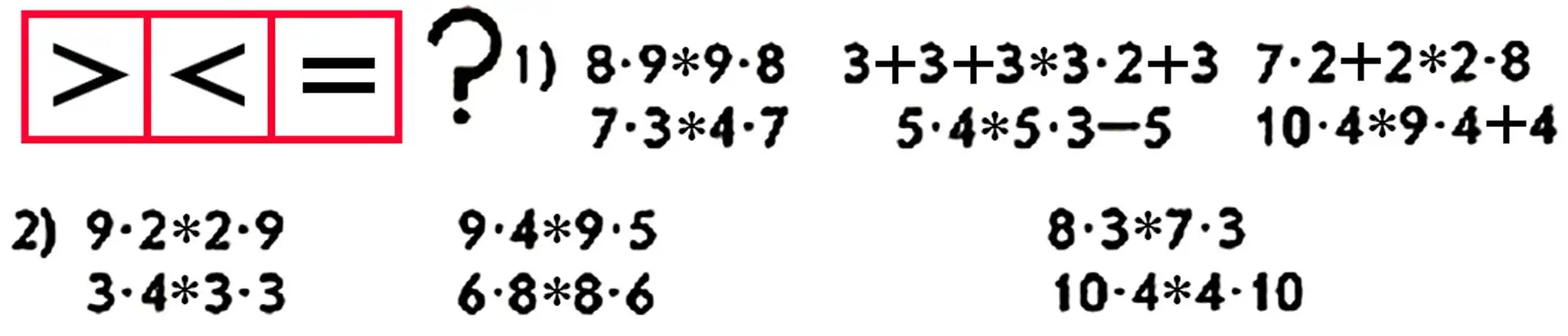
15. Create and solve examples following the pattern:
|
7*3=21 |
6*4= |
18:6=3 |
20:2 = |
|
3*7=21 |
3*6=18 |
• •• |
|
|
21:7=3 |
••• |
6-3=18 |
• •• |
|
21:3=7 |
• •• |
18:3=6 |
• •• |
|
16. 35:7= |
48:6= |
27:3= |
40:8= |
|
7*5=35 |
8*6=48 |
3*9=27 |
5*8=40 |
|
17. Solve the examples in the first row, then the second and third: |
|||
|
3*5 |
5*3 |
15:3 |
15:5 |
|
7*2 |
2*7 |
14:7 |
14:2 |
|
10*3 |
3*10 |
30:10 |
30:3 |
|
с |
10 |
5 |
||
|
6 |
6 |
10 |
||
|
4-6 |
12 |
20 |
30 |
50 |
|
а |
10 |
8 |
||
|
b |
6 |
3 |
||
|
а-b |
2 |
5 |
6 |
4 |
19. Write mathematical expressions:
1) sum of numbers 7 and 8, 15 and a, a and 10, a and c;
2) difference of numbers 24 and 5, 30 and 18, 40 and 6, c and k;
3) product of numbers 15 and 3, b and 5, b and c;
4) quotient of numbers 6 and 2, a and 3, a and k;
5) from the sum of a and & subtract the number c;
6) subtract the sum of numbers a and c from the number k.
20 .1) Write down the sum of numbers c and k. Calculate the value of the sum if:
1) c=26, k=38 2) c=26, k=37
3) с=26, k=36 4) с=26, k=3 5
2) Write down the difference between numbers a and b. Calculate the values of the difference if:
1) a=83, b = 54 2) а=83, b=55
3) а=83, b=56 4) а=83, b=57
22. 12—k. Choose 5 values for the letter k and calculate the values of the difference. Can the letter k take values 11, 12, 13, 14, 15, or 0?
23. From the series of numbers 0, 1, 2, 3, 4, 5, 6, choose values for the letter k for which the following inequalities are true: 1) k + 16 < 20, 2) 7 - k > 3.
24. Choose values for the letters and solve the problems:
1) In a book with pages. A student read В pages. How many pages does she have left to read?
2) In the class, there were с rulers, and there were k more compasses. How many compasses were there?
25. Solve the problems, formulate two reverse problems for each, and solve them: 1) In two piles, there are 96 boards. In one of them, there are 49 boards. How many boards are in the other pile?
2) Sasha walked 45 steps from home to the well, and he still has to walk 39 steps. How many steps from home to the well?
3) One glazier glazed 15 frames, and another 10. How many more frames did the first glazier glaze than the second one?
4) To the mill from the collective farm, they brought 42 sacks of wheat, 6 sacks less than rye. How many sacks of rye were brought to the mill?
26. From the forest, 27 large logs need to be taken out. The tractor takes 9 logs each time. How many times does the tractor need to go to the forest for logs?

27. How many legs do two storks have? Three frogs?
28. A seamstress sewed 3 dresses with 6 buttons each. How many buttons did she sew in total?
29. For the kindergarten, 3 boxes of pencils were bought, with 6 in each box. How many pencils were bought?
30. Tolya collected 18 dragonflies for his collection and placed them equally in 3 boxes. How many dragonflies were in each box?
31. How many boxes will be needed to pack 40 kg of cookies, 10 kg in each?
32. Formulate equations for the problems and solve them:
1) There were 20 asters in the flower bed in the morning. During the day, several more bloomed, and by the evening, there were 29. How many asters bloomed during the day?
2) When a second hose was connected to the rubber hose, the length became 20 arshins. What length of hose was connected?

3) Father caught 12 perch. When mother cooked fish soup, there were still 7 perch left. How many perch went into the soup?
4) There were 15 birds on the feeder. When some of them flew away, 4 birds remained on the feeder. How many birds flew away?
5) When 18 boats left the boathouse, there were still 9 boats left at the dock. How many boats are there in total at the boathouse?
6) For the roof repair, nails were prepared. When 14 kg of nails were used, there were still 5 kg left. How many kilograms of nails were prepared?
7) What number should be divided by 2 to get 6?
8) What number should be multiplied by 4 to get 8?
9) Which number should 10 be divided by to get 2?
10) Which number should 10 be multiplied by to get 30?
33. Write the problem briefly in the table and solve it:
1) A cup of tea costs 3 cents. How much do 4 cups of tea cost?
2) 2 .i of silk cost 8 rubles. How much does a meter of silk cost?
34. A button costs 3 cents. How much does a dozen buttons cost?
35. There were 17 kg of oil in the store. An additional 36 kg were brought. 48 kg of oil were sold during the day. How much oil is left?
36. In the workshop, there were 56 men, and there were 38 fewer women. How many people worked in the workshop?
37. Farmers mowed 35 stacks of clover in one field, and in the second, there were 8 stacks more than in the first. How many stacks of clover did the farmers mow in these two fields?
38. The height of the cabinet is 18 dm, the table is 11 dm lower than the cabinet, and the chair is 3 dm lower than the table. What is the height of the chair?
39. A goose weighs 5 kg, a piglet is 8 kg heavier than a goose, and a calf is 37 kg heavier than a piglet. How much does the calf weigh?
40. In the collective farm, there are 20 tractors. 9 went to plow, 8 to sow, and the rest were in repair. How many tractors were in repair?
41. In the workshop, there was a piece of wool 24 meters long. 9 meters were used to sew dresses. How many meters of wool were used less than remained in the piece?
42. At the construction site of the house, 24 painters worked. 5 painters were transferred to another job. How many more painters remained than were transferred to another job?
43. In the first squad, there were 34 pioneers, in the second 28, and in the third, there were 30 pioneers less than in the first and second together. How many pioneers were in the third squad?
44. For the repair of the house, 18 logs were brought on the first day, on the second day, 3 more than on the first, and on the third day, as many logs as on the first and second days together. How many logs were brought on the third day?
45. 36 first-graders went to the theater, and the same number of second-graders. In total, 38 boys went to the theater. How many girls went to the theater?
46. Two cans of milk were brought to the store: one had 48 liters, and the other the same. 67 liters of milk were sold. How many liters of milk still need to be sold?
47. Formulate problems based on the expressions:
|
91-17 |
(12+45)-6 |
(20-8)+25 |
(40-9)+40 |
|
8:2 |
(37+4)4-37 |
30-(8+9) |
(30+6)—17 |
48. Draw segments: one 27 mm long, the other 3 mm shorter. What is the length of the second segment?
49. Draw two segments: the length of the first is 34 mm, it is 3 mm shorter than the second. What is the length of the second segment?
50. Compare segment SK with segments AE using a compass,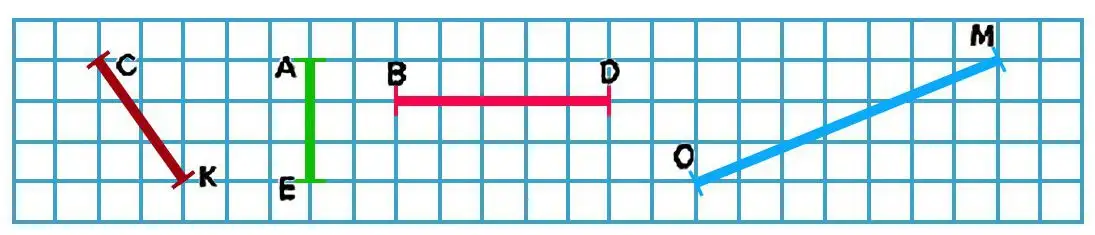
51. How many triangles are there on the drawing? Quadrilaterals?
52. What are these figures called? Measure their sides. Find right angles and write down their names.

53. Draw two such triangles. Cut them out and form a square from them.

Rose Belote
It’s the best time to make some plans for the future and it’s
time to be happy. I’ve read this post and if I could I
want to suggest you few interesting things or tips.
Perhaps you can write next articles referring to this article.
I want to read even more things about it!
أنابيب uPVC
I loved as much as you’ll receive carried out right here. The sketch is attractive, your authored material stylish. nonetheless, you command get bought an nervousness over that you wish be delivering the following. unwell unquestionably come more formerly again as exactly the same nearly a lot often inside case you shield this hike.